二叉查找树
二叉查找树
1、二叉查找树:又称二叉排序树/二叉搜索树,其任意节点与其左右子节点的大小关系都有
左 < 中 < 右,其中序遍历会得到一个递增序列,常用于元素的排序和查找,如下图
2、查找元素:二叉查找树是以二分查找为原型的数据结构,因此其查找操作的时间复杂度为 $O(\log_2 n)$ 。其查找元素的动作为从根节点起,如果要查找的值比根小,则继续查找左子树,否则查找右子树
3、插入元素:与查找元素类似。如在下面的二叉查找树中插入新元素 $12$ ,应放在元素 $11$ 的右子节点处(从根节点依次比较 $12$ 与 $10$、$13$、$11$ 的关系)
4、删除元素:实质是保持中序遍历(即递增序列)的顺序不变从中删除节点,重点在于如何填补空缺。如下图展示了三棵二叉树,分别代表三种删除情景:情景一要删除节点 $6$(只有一边子树),可以直接将子树整体上移;情景二要删除节点 $7$(两边都有子树),可以将其中序遍历的前/后一个节点(即节点 $6$ 或 $8$)填充到此处;情景三要删除节点 $10$,如果选择填充节点 $14$(其仍有子树),则还应递归处理 $14$ 的空缺(按照前两种情景选择方法处理)

#include <iostream> #include <memory> using namespace std; // 树的节点的数据类型 typedef int ElemType; // 树的节点 typedef struct BinarySearchTree { ElemType value; // 存储的数据 shared_ptr<BinarySearchTree> left, right; // 指向左子节点、右子节点 // 构造函数 BinarySearchTree(ElemType val) : value(val), left(nullptr), right(nullptr) { } } Node;代码实现:查找
// 查找数据 shared_ptr<Node> Search(shared_ptr<Node> root, ElemType key) { shared_ptr<Node> cursor = root; // 如果未遍历到最后 while (cursor != nullptr) { // 如果相同,返回当前元素 if (key == cursor->value) return cursor; // 如果所查找元素更小,则向左子树查找 else if (key < cursor->value) cursor = cursor->left; // 如果所查找元素更大,则向右子树查找 else cursor = cursor->right; } // 未找到 return nullptr; }代码实现:插入
// 插入数据:返回 bool 值表示是否插入成功 bool Insert(shared_ptr<Node> root, ElemType key) { // 一个元素为 key 的节点 shared_ptr<Node> newNode = make_shared<Node>(key); // 如果为空树,当前节点作为该空树的根节点 if (root == nullptr) { root = newNode; return true; } // 查找插入位置,cursor 用于辅助查找,parent 记录将插入在谁之下 shared_ptr<Node> cursor = root, parent = nullptr; while (cursor != nullptr) { parent = cursor; // 如果相同,返回 false,当前元素已存在 if (key == cursor->value) return false; // 如果所查找元素更小,则向左子树查找 else if (key < cursor->value) cursor = cursor->left; // 如果所查找元素更大,则向右子树查找 else cursor = cursor->right; } // 执行插入操作 if (key < parent->value) parent->left = newNode; else parent->right = newNode; // 返回 true,表示插入成功 return true; }代码实现:删除
// 删除数据:返回 bool 值表示是否删除成功 bool Remove(shared_ptr<Node> root, ElemType key) { if (root == nullptr) return false; // 查找删除位置,cursor 用于辅助查找,romoveNode 为待删除节点,parent 为其父节点 shared_ptr<Node> removeNode = nullptr, parent = nullptr, cursor = root; while (cursor != nullptr) { if (key == cursor->value) { removeNode = cursor; break; } parent = cursor; if (key < cursor->value) cursor = cursor->left; else cursor = cursor->right; } // 找不到待删除节点,返回 false, if (removeNode == nullptr) return false; // 待删除节点有一边子树为空 或 两边都为空(也适用) if (removeNode->left == nullptr || removeNode->right == nullptr) { shared_ptr<Node> fixNode = nullptr; // 待删除节点的替代节点 // 待删除节点左子树为空,用其右子树替代;右子树为空,用其左子树替代 if (removeNode->left == nullptr) fixNode = removeNode->right; else fixNode = removeNode->left; // 删除并替换节点 if (parent != nullptr) { if (parent->left == removeNode) parent->left = fixNode; else parent->right = fixNode; } // 否则 parent 为空,说明删除的是根节点,fixNode 就是新的根节点 else root = fixNode; } // 待删除节点左右子树都存在,则按照中序遍历查找该节点的替代节点(中序遍历顺序中的前一个或后一个节点) // 中序遍历顺序中的前一个节点,即待删除节点左子树的最下层的右子节点;后一个节点,即待删除节点右子树的最下层的左子节点 else { // fixNode 为待删除节点的替代节点,fixNodeParent 为替代节点的父节点 shared_ptr<Node> fixNode = removeNode, fixNodeParent = parent; // 查找前一个节点,即左子树的最下层的右子节点(也可以自行实现,查找使用后一个节点替换) cursor = removeNode->left; while (cursor != nullptr) { fixNodeParent = fixNode; fixNode = cursor; cursor = cursor->right; } // 如果替代节点仍然有左/右子树,那么递归处理替代节点,即在 fixNodeParent 这棵子树中删除 fixNode(执行后这两个节点的链接断开) Remove(fixNodeParent, fixNode->value); // 替换待删除节点 if (parent != nullptr) { if (parent->left == removeNode) parent->left = fixNode; else parent->right = fixNode; } // 否则 parent 为空,说明删除的是根节点,fixNode 就是新的根节点 else root = fixNode; // 替换节点的左右子树,指向被删除节点的左右子树 fixNode->left = removeNode->left; fixNode->right = removeNode->right; // 断开被删除节点的左右子树链接 removeNode->left = nullptr; removeNode->right = nullptr; } // 返回 true,表示删除成功 return true; }
AVL 树
AVL 树
1、AVL 树:又称平衡二叉树,是二叉查找树的一种改进形式。其任意节点的左右子树高度差不超过 1,且仍拥有二叉查找树的节点大小关系,如下图
2、插入或删除元素时,会动态调整树的结构,以便提高下次的搜索效率(解决了二叉查找树搜索次数不均衡,最极端情况下甚至会变为链表的问题)
3、其代码实现如下,平衡因子(值为 $-1$ / $0$ / $1$)为左子树高度减去右子树高度。其插入和删除操作需要调整最小不平衡树(即平衡因子的绝对值大于 $1$ 的子树),平衡的方法便是进行对应方案的旋转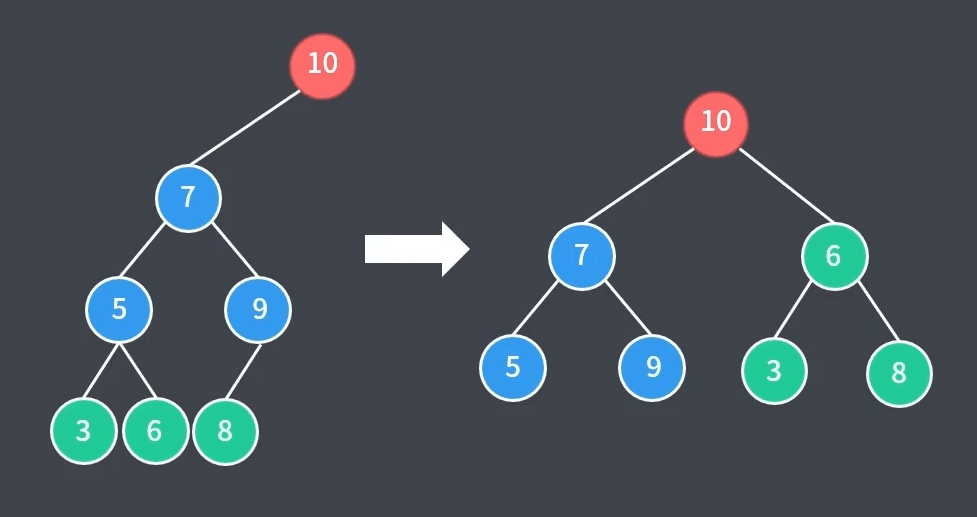
#include <iostream> #include <memory> using namespace std; // 树的节点的数据类型 typedef int ElemType; // 树的节点 typedef struct AVLNode { ElemType value; // 存储的数据 shared_ptr<AVLNode> left, right; // 指向左子节点、右子节点 int balance; // 平衡因子 } Node;平衡旋转方案
1、右单旋转:LL 平衡旋转,第一个 $L$ 表示当前节点($11$)的左子节点($8$),第二个 $L$ 表示左子节点($8$)的左子树($7$)不平衡。这种情况下进行右单旋转(向右旋转一次),如下图
2、左单旋转:RR 平衡旋转,第一个 $R$ 表示当前节点($14$)的右子节点($15$),第二个 $R$ 表示右子节点($15$)的右子树($16$)不平衡。这种情况下进行左单旋转(向左旋转一次),如下图
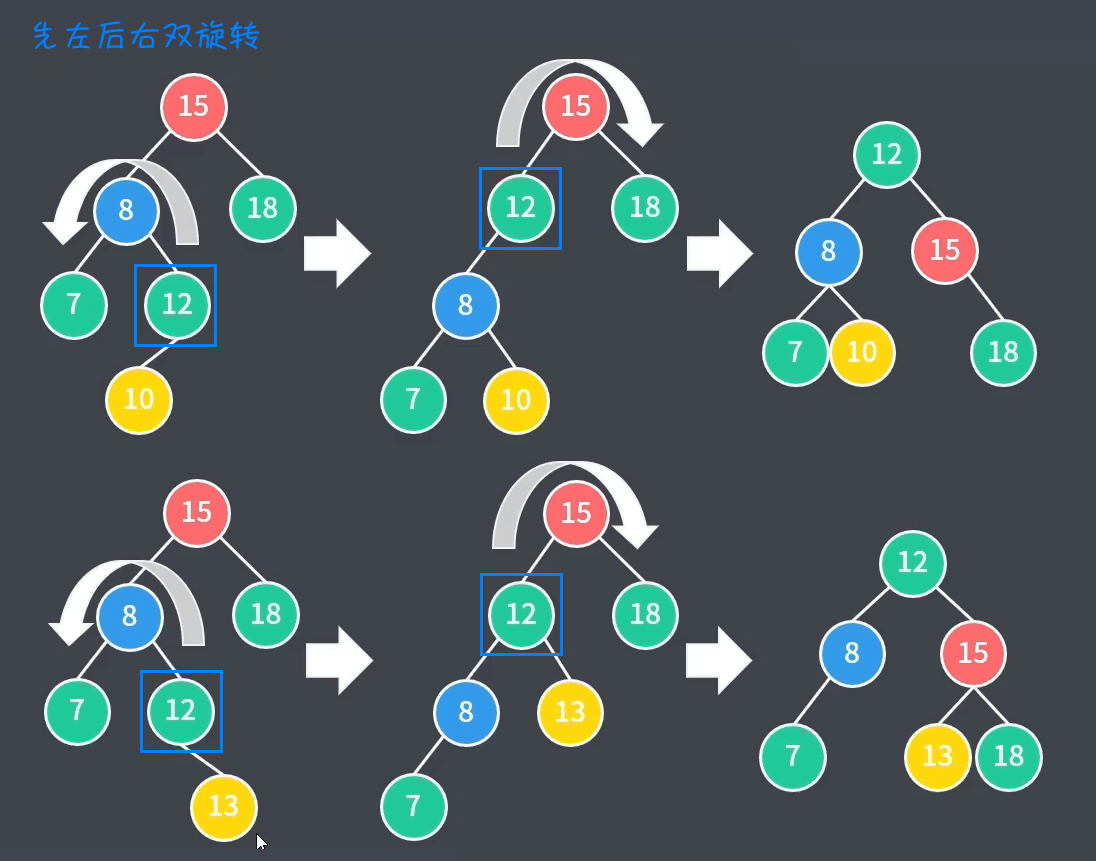
3、先左后右双旋转:LR 平衡旋转,第一个 $L$ 表示当前节点($15$)的左子节点($8$),第二个 $R$ 表示左子节点($8$)的右子树($12$ - 左$10$/右$13$)不平衡。这种情况下进行先左后右双旋转(先向左旋转一次,再向右旋转一次),如下图
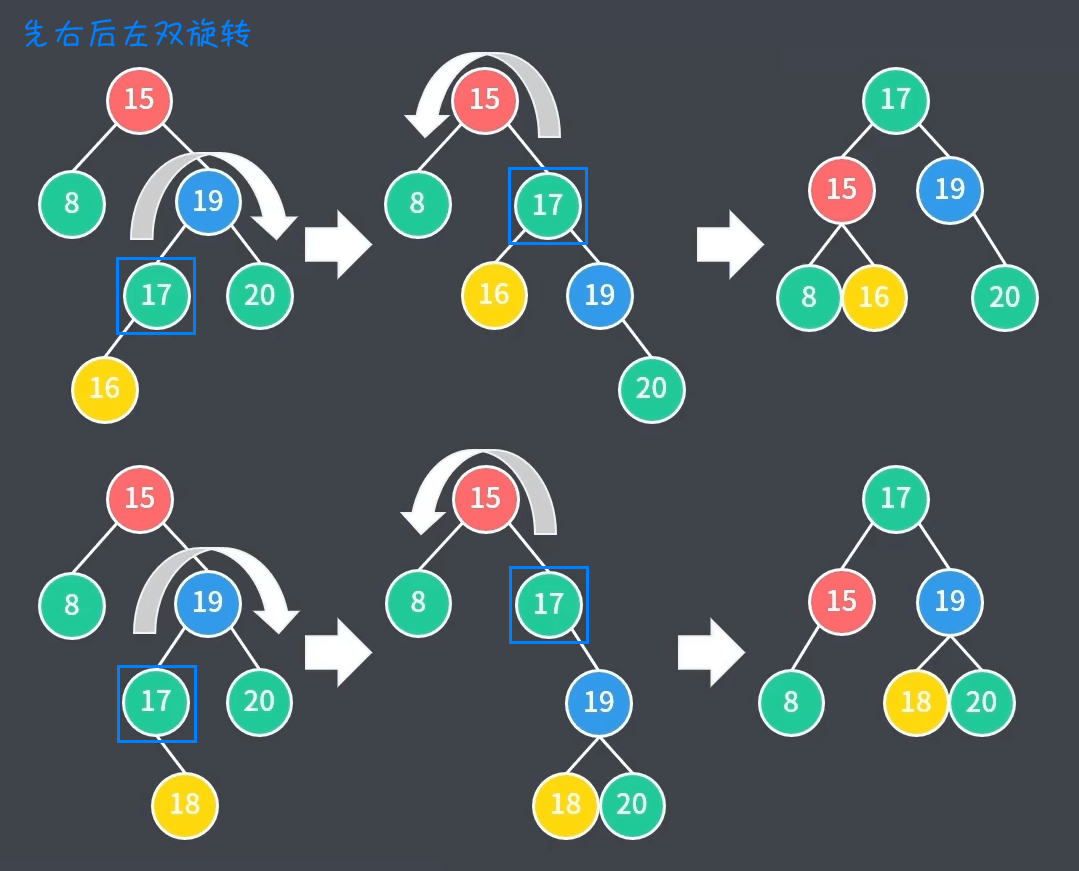
4、先右后左双旋转:RL 平衡旋转,第一个 $R$ 表示当前节点($15$)的右子节点($19$),第二个 $L$ 表示右子节点($19$)的左子树($17$ - 左$16$/右$18$)不平衡。这种情况下进行先右后左双旋转(先向右旋转一次,再向左旋转一次),如下图
5、所旋转的节点都是第一个字母指代的节点,即当前节点的左/右子节点,将其提升为父节点;其余节点如果能跟随旋转(且不影响大小关系)则直接跟随,否则重新安排合适位置
哈夫曼树
哈夫曼树
1、哈夫曼树:又叫最优二叉树,指带权路径长度最短的树。含有 $n$ 个带权叶子节点的二叉树中,带权路径长度最短(WPL 最短)的二叉树,称为最优二叉树或哈夫曼树
2、权指对实体(节点/边)属性的数值化描述;节点带权路径长度指节点到根的路径长度与节点的权的乘积;树的带权路径长度(WPL)指树中所有叶子结点的带权路径长度之和
3、同一棵树可能有多种哈夫曼树,其不是唯一的。如下图,列出了同一棵树不同排列下的带权路径长度计算,其中第 $2$、$3$ 棵都为哈夫曼树#include <iostream> using namespace std; // 动态分配数组存储 // 树的节点 typedef struct HTNode { int weight; // 节点的权值 int parent, left, right; // 节点的父节点和子节点下标 } Node;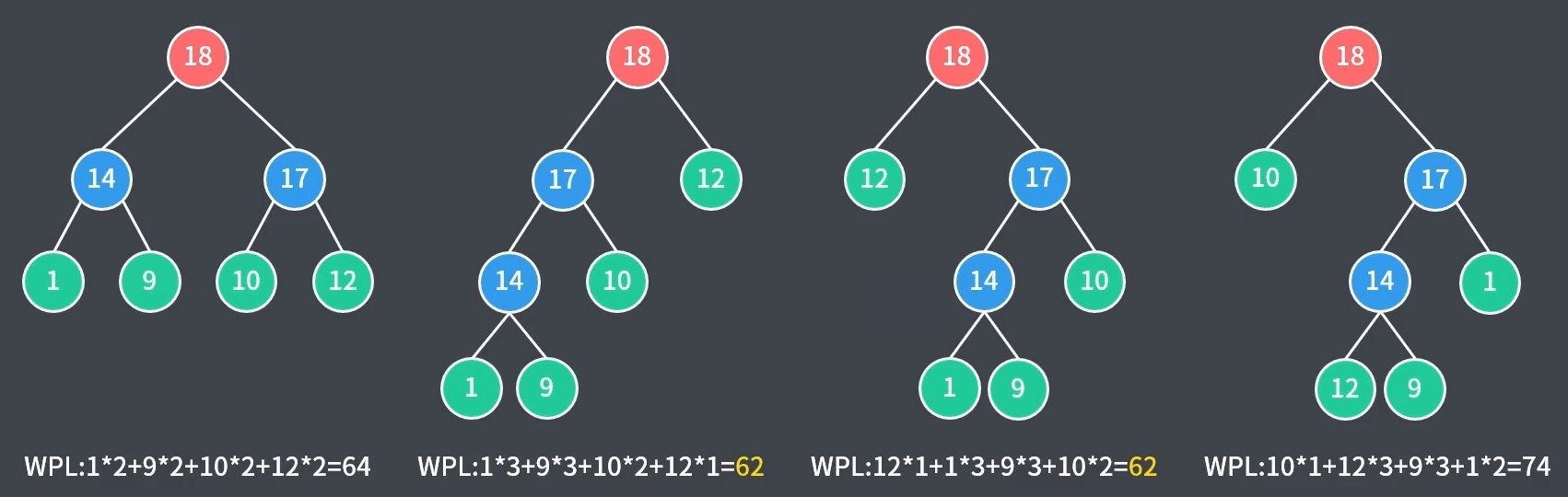
构造哈夫曼树
1、将所有节点看作仅含一个节点的树,则所有树构成了森林
2、创建新节点,选择两个权值最小的树作为其左右子树,新节点权值为二者之和
3、将构成的新树放回森林中,重复上述步骤直到只剩一棵树为止
4、规律:权值越大的节点越靠上,这样节点到根的路径更短,因此该节点带权路径长度也更短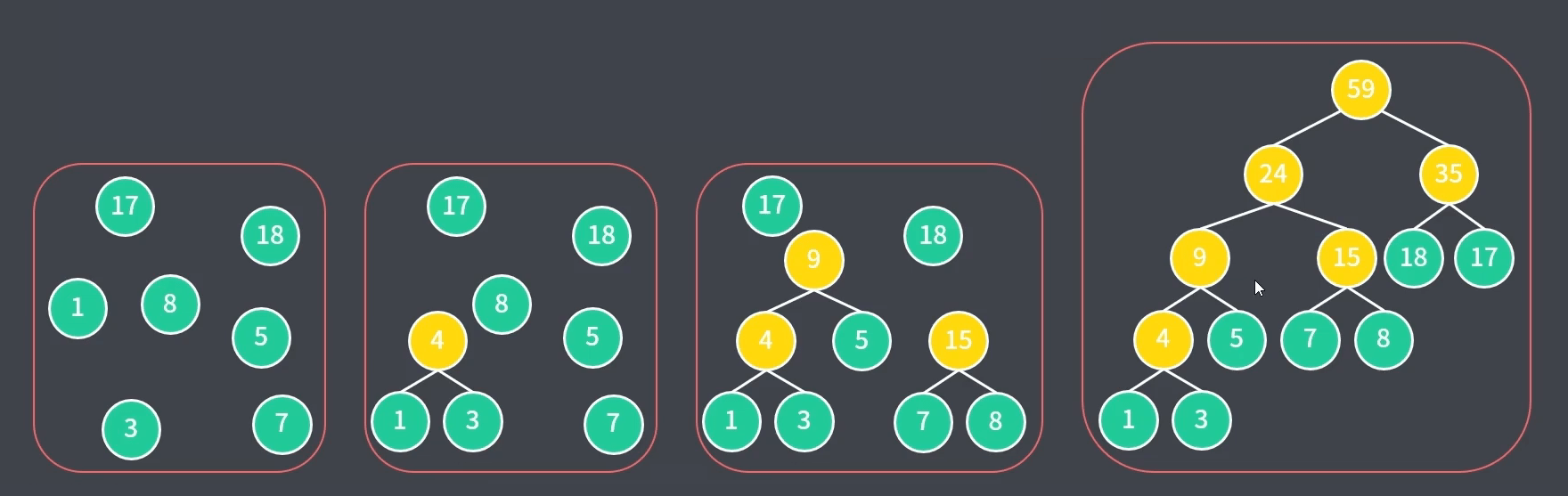
哈夫曼编码
引入
1、哈夫曼编码是一种对字符编码进行压缩和解析的方式标准,如下图给出了一个例子
2、其中,固定长度编码保留了完整的 ASCII 码信息,但传输时过于繁琐,因此我们可以在编码中对前缀 $0$ 进行压缩,即可变长度编码
3、但可变长度编码解析时,难以确定前缀 $0$ 的个数和分组区别,解析十分困难。其中的原因之一是:压缩后的字符编码可能是另一编码中的一部分(如 $48$ 压缩后的 $110000$ 是 $97$ 压缩后的 $1100001$ 的一部分),这便难以分组
4、这时,需要一种既能压缩也能解析的编码方式,这便是哈夫曼编码(前缀编码)。其任意两个字符的编码,不能是对方的前缀。
哈夫曼编码与哈夫曼树
1、树的每个节点都是唯一的,根节点到叶子结点的路径也是唯一的。令哈夫曼树的叶子节点代表不同的字符,左右分支分别标记 $0$ 和 $1$,那么,根节点到叶节点的路径就构成了一个二进制编码,如下图
2、根节点到叶节点的路径代表了编码的长度,节点的权值即字符(在电文/数据/字符集中)出现的次数,这样,电文的总长度即为 WPL
3、由于哈夫曼树中权值越大的节点越靠上,所以出现频率高的字符,其编码也更短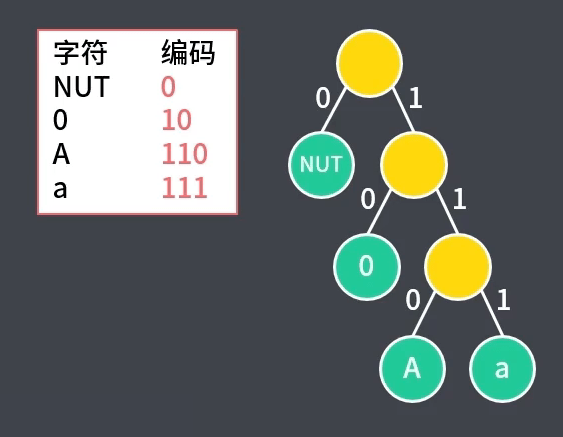



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试