Dijkstra 单源带权(朴素)
Dijkstra 朴素算法
1、最短路 1:给定 $n$ 个点 $m$ 条边的有向图($n \leq 10^3, m \leq 10^5$),输出点 $1$ 到 $n$ 的最短距离。对于 $m$ 条边,每次输入 $u、v、w$ ,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的有向边。如果不存在路径,输出 $-1$
2、先前在图与回溯中介绍过无权最短路,现在有了权值,需要做一个结构体保存。Dijkstra还使用一个数组 $d[]$ ,$d[i]$ 表示从起点 $st$ 到 $i$ 的最短距离
3、Dijkstra 思路如下图:起始时,建图,标记所有 $d[i]$ 为 $\infty$,以 $1$ 为起点,向外走一层,将经过的边松弛(用边的权值更新所到点的 $d[i]$ ,$d[i]$ 取较小值);接下来,比较得到最小的 $d[i]$ ,以该点为当前起点(图中为点 $2$),先前的点已经可以忽略,继续向外走一层,将经过的边松弛(注意,$d[3]$ 取较小值更新为 $3$);以此类推,以 $4$ 为当前起点发现点 $4$ 没有出点,返回;以 $3$ 为当前起点,走到终点,更新 $d[5]$ 为 $6$,所以最短路为 $6$
4、该算法结合了贪心和DP的思想,每个点只拓展一次,且拓展时已为最短距离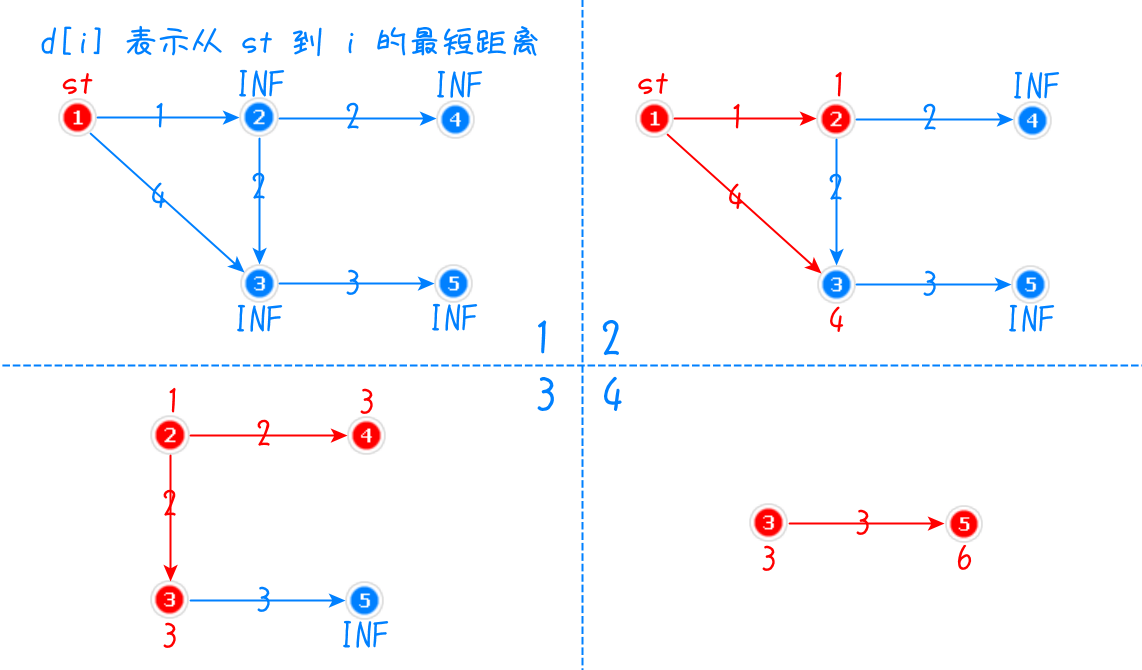
代码实现
#include <bits/stdc++.h> using namespace std; // 一个十六进制的 3f 对应二进制的 0011 1111 (恰好 8 bit = 1 Byte),因此 int 写 4 个 3f // 用 3f 表示无穷的好处是,该值可以安全地乘 2 或做一些运算而不溢出 const int INF = 0x3f3f3f3f; const int N = 2e5 + 10; // 出边 struct Edge { // x 表示出点,w 表示权值 int x, w; }; vector<Edge> g[N]; // g 是一个 vector<Edge> 的数组 int d[N]; // d[i] 表示从起点 st 到 i 的最短距离 int n, m; // Dijkstra 朴素 void Dijkstra(int st) { memset(d, INF, sizeof(d)); // 初始化 d[i] 为 INF d[st] = 0; // 起始点 d[st] 为 0 bitset<N> vis; // 标记是否拓展过 // 进行 n 轮检验 for (int i = 1; i <= n; i++) { // 找出 d[i] 最小点 u int u = 1; for (int j = 1; j <= n; j++) // 如果当前的点 u 未被拓展(被拓展过就必须更换) 或 (d[j] < d[u] 且 j 未被拓展) if (vis[u] || !vis[j] && d[j] < d[u]) u = j; // 此时 u 点为 d[i] 最短点,d[u] 为当前最优长度 // 从 u 点向下松弛,开始拓展,标记 vis[u] vis[u] = true; // 遍历所有 u 的出边 for (auto &[v, w] : g[u]) // 如果 v 未被拓展 且经 u 到 v 的总距离比原先(可能的) d[v] 更短 if (!vis[v] && d[u] + w < d[v]) d[v] = d[u] + w; // 更新 d[v] } } void solve() { cin >> n >> m; for (int i = 1; i <= m; i++) { int u, v, w; cin >> u >> v >> w; // 判断不是自环 if (u != v) g[u].push_back({v, w}); // 存储有向图 } Dijkstra(1); cout << (d[n] != INF ? d[n] : -1); } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Dijkstra 单源带权(堆优化)
Dijkstra 堆优化
1、最短路 2:给定 $n$ 个点 $m$ 条边的有向图($n,m \leq 2 \times 10^5$),输出点 $1$ 到 $n$ 的最短距离。对于 $m$ 条边,每次输入 $u、v、w$ ,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的有向边。如果不存在路径,输出 $-1$
2、数据量变大,原先的朴素算法中由于有 $O(n^2)$ 会超时,可以用优先队列(堆)优化程序。优先队列中存储点和起点到该点的总距离,设定为小根堆,确保堆顶元素的总距离最短,因此堆顶即为每次 $d[i]$ 最小的点,便不需要查找了,复杂度优化为 $O(m \log n)$
3、起始,将起点入队,每次获取起点(且从队中弹出)并向外走一层,像朴素算法一样将边松弛(维护 $d[i]$),同时将新点入队。只要队列不为空,就继续执行这一过程代码实现
#include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f3f; const int N = 2e5 + 10; // 出边 struct Edge { // x 表示出点,w 表示权值 int x, w; }; // 定义 < 比较规则 bool operator<(const Edge &u, const Edge &v) { // 注意:优先队列通过 < 成立得到大根堆,所以需要小根堆则在比较中应使用 > 比较 // 用 > 比较 w,保证堆顶元素 w 最小(总路径最短) return u.w > v.w; } vector<Edge> g[N]; // g 是一个 vector<Edge> 的数组 int d[N]; // d[i] 表示从起点 st 到 i 的最短距离 int n, m; // Dijkstra 堆优化 void Dijkstra(int st) { memset(d, INF, sizeof(d)); // 初始化 d[i] 为 INF d[st] = 0; // 起始点 d[st] 为 0 bitset<N> vis; // 标记是否拓展过 // 使用优先队列(堆)优化,需要定义 Edge 的 < 比较规则,小根堆 priority_queue<Edge> pq; // pq 中的 w 表示从起点到当前点的总距离 pq.push({st, d[st]}); // 初始化 pq,将起点入队 // pq 不为空,能够找到新的点就继续循环 while (!pq.empty()) { int x = pq.top().x; // 取出堆顶元素(w 最小)的 x 作为起点(即朴素算法中查找 d[i] 最小的点) pq.pop(); // 弹出当前点 // 如果拓展过,就跳过 if (vis[x]) continue; vis[x] = true; // 标记当前点被拓展 // 遍历当前最小点 x 的所有出边,向外走一层 for (auto &[y, w] : g[x]) { // 如果 y 未被拓展 且经 x 到 y 的总距离比原先(可能的) d[y] 更短 if (!vis[y] && d[x] + w < d[y]) { // 不能在此处标记 vis[y],否则 d[y] 之后将无法更新 d[y] = d[x] + w; // 更新 d[y] pq.push({y, d[y]}); // 当前 y 点入队 } } } } void solve() { cin >> n >> m; for (int i = 1; i <= m; i++) { int u, v, w; cin >> u >> v >> w; // 判断不是自环 if (u != v) g[u].push_back({v, w}); // 存储有向图 } Dijkstra(1); cout << (d[n] != INF ? d[n] : -1); } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Floyd 全源最短路
Floyd 全源最短路
1、最短路 3:给定 $n$ 个点 $m$ 条边的有向图($n \leq 300, m \leq 10^5$),有 $q$ 次询问,每次输入 $u\ v$,输出从 $u$ 到 $v$ 的最短距离(若不存在则输出 $-1$)。对于 $m$ 条边,每次输入 $u、v、w$ ,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的有向边,再给出这 $q$ 次询问,每次输入所询问的 $u\ v$
2、该题询问任意两点的最短距离,是多源最短路。Floyd 的证明较为复杂,因此在此只介绍用法,当作模板背过即可。对于图中任意两点 $i, j$,定义 $d[i][j]$ 表示 $i$ 到 $j$ 当前的最短距离,但我们并不关心两点间的路径;我们使用三层循环,最外层遍历一个中转点 $k$,内两层分别遍历起点 $i$ 和终点 $j$,则有结论 $d[i][j] = d[i][k] + d[k][j]$ ($i$ 到 $j$ 的距离 $= i$ 到 $k$ 的距离 $+ k$ 到 $j$ 的距离),再将该结果与原先 $d[i][j]$ 取较小值更新 $d[i][j]$ 。全部操作后,$d[i][j]$ 便直接是最短路径长度
3、这只是一个非常宏观的结论(因为根本不关心具体路径如何),把结论背过即可。注意:起始应使用邻接矩阵建图,且该图也直接充当 $d[][]$ 数组,在其上更新数据;开始时需要初始化数组为无穷,初始化自环距离为 $0$;输入可能有重边,取更短值;特别注意,必须最外层枚举中转点 $k$ ,其次是 $i$ ,再其次是 $j$ ,否则结论不成立。该算法时间复杂度为 $O(n^3)$代码实现
#include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f3f; const int N = 310; int d[N][N]; // 邻接矩阵 兼 处理最短路的数组 int n, m, q; // Floyd 算法 void Floyd() { // 默写结论,注意枚举时 k 在最外层 for (int k = 1; k <= n; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) d[i][j] = min(d[i][j], d[i][k] + d[k][j]); } void solve() { cin >> n >> m >> q; // 初始化 d 数组为无穷 memset(d, INF, sizeof(d)); // 初始化自环距离为 0 for (int i = 1; i <= n; i++) d[i][i] = 0; // 输入并建图 for (int i = 1; i <= m; i++) { int u, v, w; cin >> u >> v >> w; d[u][v] = min(d[u][v], w); // 可能有重边,取较小值 } Floyd(); while (q--) { int u, v; cin >> u >> v; cout << (d[u][v] != INF ? d[u][v] : -1) << '\n'; } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Bellman-Ford 单源负权
Bellman-Ford 单源负权最短路
1、最短路 4:给定 $n$ 个点 $m$ 条边的有向图($n,m \leq 10^4$),输出点 $1$ 到 $n$ 的最短距离。对于 $m$ 条边,每次输入 $u、v、w$ ,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的有向边($w$ 可能为负)。如果图中存在负环,只输出 $-1$
2、Bellman-Ford 并不基于先前的搜索算法,而是基于循环枚举,因为负环内会越转总距离越小,搜索会不断转圈而死循环。该算法流程为:枚举所有边 $n-1$ 次,每次在过程中对所有边松弛(用 $d[x]$ 更新 $d[y]$),至 $n-1$ 次操作完成后便得到了最短路,此处取 $n-1$ 次是因为最坏情况下(图为一条链时),最多只需要 $n-1$ 次便可以使所有边都被松弛。接下来,多枚举所有边一次,因为前 $n-1$ 次一定所有边都至少被松弛过一次且得到了最短的距离,若该次还有边可以被松弛则说明出现了负环(因为负环内会越转总距离越小)
3、实现上,外层可以直接循环 $n$ 次,用变量 $circle$ 记录是否有负环,每次外层循环开始时初始化为 false,内层有边被松弛时更新 $circle$ 为 true,这样使得 $circle$ 的值只取决于第 $n$ 次循环(即多进行的一轮枚举),便可以判断负环。由于该算法不需要使用严格的点的出点(不需要方向性),只需要点和边的关系,所以在建图时可以直接记录点和边的三元组建图(像先前使用邻接表建图也可以,只是内层枚举时要用两层循环分别枚举点和出点)。该算法时间复杂度为 $O(nm)$代码实现
#include <bits/stdc++.h> using namespace std; using ll = long long; const int N = 2e5 + 10; const ll INF = 2e18; int n, m; bool circle; // 标记负环 ll d[N]; // d[i] 记录从起点到 i 的最短距离 // 存三元组边,建图 struct Edge { ll u, v, w; }; vector<Edge> es; // Bellman-Ford 单源负权 void Bellman_Ford() { // 初始化(由于 memset 只接受 int 范围,所以用循环) for (int i = 1; i <= n; i++) d[i] = INF; d[1] = 0; // 外层进行 n 轮松弛,判断第 n 轮是否进行了松弛 for (int i = 1; i <= n; i++) { // 还原 circle,使 circle 只受最终的第 n 轮的影响 circle = false; // 内层进行一轮松弛,枚举所有点和边 for (auto &[x, y, w] : es) // 如果可以被松弛 if (d[x] + w < d[y]) { d[y] = d[x] + w; circle = true; // 标记进行了松弛操作 } } } void solve() { cin >> n >> m; for (int i = 1; i <= m; i++) { ll u, v, w; cin >> u >> v >> w; es.push_back({u, v, w}); } Bellman_Ford(); // 如果 circle 为 true,有负环 if (circle) cout << "-1"; else for (int i = 1; i <= n; i++) cout << d[i] << ' '; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
SPFA 队列优化
SPFA 队列优化
1、最短路 4:给定 $n$ 个点 $m$ 条边的有向图($n,m \leq 10^4$),输出点 $1$ 到 $n$ 的最短距离。对于 $m$ 条边,每次输入 $u、v、w$ ,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的有向边($w$ 可能为负)。如果图中存在负环,只输出 $-1$
2、SPFA 是 Bellman-Ford 的队列优化版本。由于原先算法在内层循环判断是否松弛时有大量多余判断,因为一些点早早就得到了最短距离而后续不再需要被更新,为了防止这一现象,可以每轮只松弛上一轮被松弛的点(当一个点被松弛后,其出点才可能需要被松弛)。SPFA 的实现不再依靠循环枚举,其使用一个队列记录被松弛到的出点,后续再将与这些点有关的边松弛
3、实现上,由于需要点与出点的关系,所以需要邻接表建图。使用队列维护点时,为了避免重复,需要一个 $inq[]$ 标记某个点是否已经在队内,当一个点被松弛后加入队列时,如果其已经在队内便不需要重复添加了(在队内的点早晚会被松弛)。由于不依靠循环枚举,因此需要一个额外的 $cnt[]$ 记录每个点被松弛的次数,如果达到 $n$ 次,说明出现负环。该算法时间复杂度不稳定,最差为 $O(nm)$,通常远低于该复杂度代码实现
#include <bits/stdc++.h> using namespace std; using ll = long long; const int N = 2e5 + 10; const ll INF = 2e18; int n, m; ll d[N]; // d[i] 记录从起点到 i 的最短距离 // 邻接表建图 struct Edge { ll x, w; }; vector<Edge> g[N]; // SPFA,其返回值表示是否有负环,st 为起点 bool SPFA(int st) { // 初始化 for (int i = 1; i <= n; i++) d[i] = INF; d[st] = 0; queue<int> q; // 存储上轮被松弛,这轮需要松弛的点 bitset<N> inq; // 标记是否在队内 int cnt[N] = {}; // 记录点被松弛的次数 q.push(st), inq[st] = true; // 只要队列不为空,就一直跑 while (q.size()) { // 取出队头,作为松弛的起点 int x = q.front(); q.pop(), inq[x] = false; // 枚举所有出点 for (auto &[y, w] : g[x]) { // 判断能否被松弛 if (d[x] + w < d[y]) { // 判断是否有负环(被松弛次数达到 n 次) if (++cnt[y] >= n) return true; d[y] = d[x] + w; // 如果不在队内,入队 if (!inq[y]) q.push(y), inq[y] = true; } } } return false; } void solve() { cin >> n >> m; for (int i = 1; i <= m; i++) { ll u, v, w; cin >> u >> v >> w; g[u].push_back({v, w}); } // 跑 SPFA,如果返回值为 true 则有负环 if (SPFA(1)) cout << "-1"; else for (int i = 1; i <= n; i++) cout << d[i] << ' '; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Johnson 全源负权
Johnson 全源负权最短路
1、最短路 5:给定 $n$ 个点 $m$ 条边的有向图($n \leq 3 \times 10^3, m \leq 6 \times 10^3$),有 $q$ 次询问,每次输入 $u\ v$,输出从 $u$ 到 $v$ 的最短距离,如果不存在通路则输出 $noway$,如果存在负环则输出 $starrycoding$。对于 $m$ 条边,每次输入 $u、v、w$ ,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的有向边($w$ 可能为负)。再给出这 $q$ 次询问,每次输入所询问的 $u\ v$
2、类比于物理中势能的概念,也可以套用在图论上,如一个点到另一个点所做的功(类比最短距离),等于两点之间的势能差。由于势能需要一个相同的零势能点,该算法假定了一个虚拟源点 $0$ 作为零势能点,为后续势能计算提供统一的起点,假定 $0$ 到所有点的距离为 $0$
3、算法首先通过 Bellman-Ford 计算出 $0$ 点(即零势能点)到所有点的最短距离,记为势能 $h[]$。接下来,修改所有边权:由于物理中势能差与中间经过的过程(类比经过的点)无关,只与起点和终点有关(即无论走哪条路径两点间势能差不变,这使得即使加上势能差,后续也可以通过减去相同的势能差还原),于是通过调整每条边的边权加上势能差 $w’ = w + h[x] - h[y]$,由于先前 Bellman-Ford 的松弛操作保证了 $h[y] \leq h[x] + w$(三角形不等式),移项可知新权值 $w’ \geq 0$,保证了新权值中不会出现负权
4、由于没有负权,便可以使用目前速度最快的单源最短路 Dijkstra,以每个点为起点分别跑一次 Dijkstra (此处也是该程序时间复杂度瓶颈),得出调整后的最短路径 $d’[x][y]$。最后,将其还原回原图的最短路径 $d[x][y] = d’[x][y] - h[x] + h[y]$ (将加上的势能差减去),得到真实的 $d[x][y]$ 即为答案
5、注意,判断是否两点不通时不能直接用 $\infty$ 判断(由于有负权,边被松弛时可能比 $\infty$ 小),可以与 $\frac{\infty}{2}$ 比较(可证明松弛过的点 $d[x][y] \lt \frac{\infty}{2}$)。此外,由于多增加了一个虚拟源点,那么 $n + 1$ 个点最坏情况需要 $n$ 次松弛才能得到最短距离,在 $n$ 次后还可以松弛才表明出现负环,因此 SPFA 判断是否负环的条件要修改为++cnt[y] > n或++cnt[y] >= n + 1,该算法时间复杂度为 $O(nm \log m)$代码实现
#include <bits/stdc++.h> using namespace std; using ll = long long; const int N = 3e3 + 10; const ll INF = 2e18; int n, m; ll h[N]; // 记录势能 ll d[N][N]; // x->y 的最短距离 // 存边,建图 struct Edge { ll x, w; }; vector<Edge> g[N]; // Dijkstra 优先队列需要小根堆,修改比较规则 bool operator<(const Edge &u, const Edge &v) { return u.w > v.w; } // Dijkstra,额外传入需要处理的 d[i],以 st 为起点,处理 d[st][] 第二维 void Dijkstra(int st, ll d[]) { // 初始化 d[st][] for (int i = 1; i <= n; i++) d[i] = INF; d[st] = 0; // 优先队列 priority_queue<Edge> pq; pq.push({st, d[st]}); bitset<N> vis; // 处理优先队列 while (pq.size()) { ll x = pq.top().x; pq.pop(); if (vis[x]) continue; vis[x] = true; // 遍历出点并松弛 for (auto &[y, w] : g[x]) { if (d[x] + w < d[y]) { d[y] = d[x] + w; pq.push({y, d[y]}); } } } // Johnson 的实现,将加上的势能差减去,还原回原图 d[][] 数组 for (int i = 1; i <= n; i++) d[i] = d[i] - h[st] + h[i]; } // SPFA,返回是否有负环,处理出势能数组 h[] bool SPFA(int st) { // 初始化 h[] for (int i = 1; i <= n; i++) h[i] = INF; h[st] = 0; queue<int> q; // 存储上轮被松弛,这轮需要松弛的点 bitset<N> inq; // 标记是否在队内 int cnt[N] = {}; // 记录点被松弛的次数 q.push(st), inq[st] = true; // 只要队列不为空,就一直跑 while (q.size()) { // 取出队头,作为松弛的起点 int x = q.front(); q.pop(), inq[x] = false; // 枚举所有出点 for (auto &[y, w] : g[x]) { // 判断能否被松弛 if (h[x] + w < h[y]) { // 判断是否有负环(被松弛次数达到 n 次) if (++cnt[y] > n) return true; h[y] = h[x] + w; // 如果不在队内,入队 if (!inq[y]) q.push(y), inq[y] = true; } } } return false; } // Johnson,返回是否存在负环 bool Johnson() { // 建立虚拟源点 0, 且 0 -> i 的 w = 0 for (int i = 1; i <= n; i++) g[0].push_back({i, 0}); // 调用 Bellman-Ford 求 0(零势能点) 到所有点的单源最短路,作为势能 h[] // 如果 SPFA 返回 true,直接返回 true 表示有负环 if (SPFA(0)) return true; // 修改所有边权 for (int x = 1; x <= n; x++) for (auto &[y, w] : g[x]) w = w + h[x] - h[y]; // 每个点跑一次 Dijkstra for (int i = 1; i <= n; i++) Dijkstra(i, d[i]); return false; } void solve() { cin >> n >> m; for (int i = 1; i <= m; i++) { ll u, v, w; cin >> u >> v >> w; g[u].push_back({v, w}); } // 跑 Johnson,返回 true 有负环 if (Johnson()) { cout << "starrycoding"; return; } int q; cin >> q; while (q--) { int x, y; cin >> x >> y; // 判断是否连通,由于有负权,与 INF /2 比较 if (d[x][y] >= INF / 2) cout << "noway" << '\n'; else cout << d[x][y] << '\n'; } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试