树的知识
认识树结构
1、树:指有层次关系的 $N$ 个节点的有限集合(如下图);对于空树,$N = 0$ ;对于非空树,有且仅有一个根。除根外,可分为多个互不相交的有限集合,称为子树
2、节点:每个数据就是一个节点。节点可分为根节点、分支节点、叶子结点。在两个节点的关系上分为前驱(父节点)和后继(子节点)
3、在树中:边用来表明两个节点之间的层次关系(父子关系);高度指的是深度(层次),树的高度指的是整个树最深的层次数,如下图 $E$ 的高度为 $3$ ,树的高度为 $4$ ;度指的是边的个数(子节点的个数),树的度指的是整个树各节点度的最大值,如下图 $A$ 的度为 $3$,$C$ 的度为$1$,树的度为 $3$
度为 $n$ 的树与 $n$ 叉树
1、度为 $n$ 的树:各节点度的最大值为 $n$,即任意节点的度 $\leq n$ ;注意,至少应有一个节点的度 $= n$
2、$n$ 叉树:树中每个节点最多有 $n$ 个子节点,即任意节点的度 $\leq n$ ;特别的,与度为 $n$ 的树不同,允许所有节点的度 $\lt n$
3、因此,度为 $n$ 的树一定可称为 $n$ 叉树,但反之不可树的性质
1、对于一个 $n$ 叉树,其第 $i$ 层至多有 $n^{i-1}$ 个节点,高度为 $h$ 的 $n$ 叉树至多有 $\frac{n^h-1}{n-1}$ 个节点(根据等比数列求和: $1 + n + n^2 + \ldots + n^{h-2} + n^{h-1}$)
2、高度为 $h$ 的 $n$ 叉树至少有 $h$ 个节点,其只有一个叉;高度为 $h$ 的度为 $n$ 的树至少有 $h + n - 1$ 个节点,其在 $n$ 叉树的基础上至少有一个节点有 $n$ 个叉,根节点重复计算了一次所以减去$1$
3、有 $m$ 个节点的 $n$ 叉树的最小高度,当所有节点都有 $n$ 个子节点时,$h = \log_n (m(n-1)+1)$
树的存储结构
双亲表示法(顺序存储)
1、描述:使用一组连续空间(数组)存储每个节点,同时每个节点中有一个伪指针,指示该节点父节点在数组中的位置
2、如上例中的树,代码实现如下,另附下表说明详细的存储情况。当parent == -1时,表示该节点为根节点#define MAX_TREE_SIZE 100 // 树的节点 typedef struct ParentTreeNode { ElemType data; // 节点存储的数据,ElemType 为数据的类型 int parent; // 伪指针:指向该节点父节点的下标 } PTNode; // 树类型 typedef struct ParentTree { PTNode nodes[MAX_TREE_SIZE]; // 用数组存储树的节点 int num; // 节点数 } PTree;index 0 1 2 3 4 5 6 7 8 9 10 11 12 data A B C D E F G H I J K O P parent -1 0 0 0 1 1 2 3 3 3 4 4 8 孩子表示法(顺序+链式)
1、描述:将每个节点的子节点都用单链表连接起来,形成一个线性结构,$N$ 个节点就会有 $N$ 个孩子链表
2、如上例中的树,代码实现如下,另附下表说明详细的存储情况
3、该结构的优势:使用链表连接孩子节点,使得访问总是能够(跨层级时)自上而下、(同层级时)自左向右按照层次访问,符合直观想象#define MAX_TREE_SIZE 100 // 树的节点 typedef struct ChildrenLinkedNode { ElemType data; // 节点存储的数据,ElemType 为数据的类型 CLNode *child; // 指针指向下一个孩子节点 } CLNode; // 树类型 typedef struct ChildrenTree { CLNode nodes[MAX_TREE_SIZE]; // 用数组存储树的节点 int num; // 节点数 } CTree;index 0 1 2 3 4 5 6 7 8 9 10 11 12 data A B C D E F G H I J K O P child B E G H K null null null P null null null null |_child C F I O |__child D J 孩子兄弟表示法(链式-二叉链表)
1、又称二叉树表示法或二叉链表表示法,即以二叉链表作为树的存储结构。链表中的节点的两个链分别指向该节点的第一个子节点(左链)和下一个兄弟节点(右链)
2、如上例中的树,代码实现如下,下图展示了这种表示方法的存储结构// 树的节点 typedef struct ChildBrotherNode { ElemType data; // 节点存储的数据,ElemType 为数据的类型 CBNode *firstChild; // 左链:指向该节点第一个子节点 CBNode *nextSibling; // 右链:指向该节点下一个兄弟节点 } CBNode;
二叉树
二叉树与满二叉树
1、二叉树:英文为Binary Tree,指节点的度 $\leq 2$ 的有序树(左右子树次序固定),如下图
2、满二叉树:指二叉树只有最后一层有叶子结点且不存在度为 $1$ 的节点(每一层只要有节点,必然扑满)
3、一个高为 $h$ 的满二叉树的节点数为 $2^h -1$。按层序从 $1$ 编号,节点 $i$ 的左子为 $2i$,右子为 $2i + 1$,父节点为 $\frac{i}{2}$;按层序从 $0$ 编号,节点 $i$ 的左子为 $2i + 1$,右子为 $2i + 2$,父节点为 $\lfloor \frac{i}{2} \rfloor$
常见的树:完全二叉树
1、完全二叉树:当且仅当二叉树每个节点的序号都与同高度的满二叉树节点序号完全对应时,称为完全二叉树(即只有最后一层可以不铺满),如下图
2、完全二叉树中,只有最后两层可能有叶子结点且最多有一个度为 $1$ 的节点
3、完全二叉树的编号与满二叉树相同,因此编号公式通用。此外,如果节点 $i \leq \frac{n}{2}$,该节点为分支节点;如果节点 $i \gt \frac{n}{2}$,该节点为叶子结点
常见的树:二叉查找树
1、二叉查找树:又称二叉排序树/二叉搜索树,其任意节点与其左右子节点的大小关系都有
左 < 中 < 右,其常用于元素的排序和查找,如下图
2、在下面的二叉查找树中插入新元素 $12$,应放在元素 $11$的右子节点处(从根节点依次比较 $12$ 与 $10$、$13$、$11$ 的关系)
常见的树:AVL 树
1、AVL 树:又称平衡二叉树,是二叉查找树的一种改进形式。其任意节点的左右子树高度差 $\leq 1$ ,且仍拥有二叉查找树的节点大小关系,如下图
2、插入或删除元素时,会动态调整树的结构,以便提高下次的搜索效率(解决了二叉查找树搜索次数不均衡,最极端情况下甚至会变为链表的问题)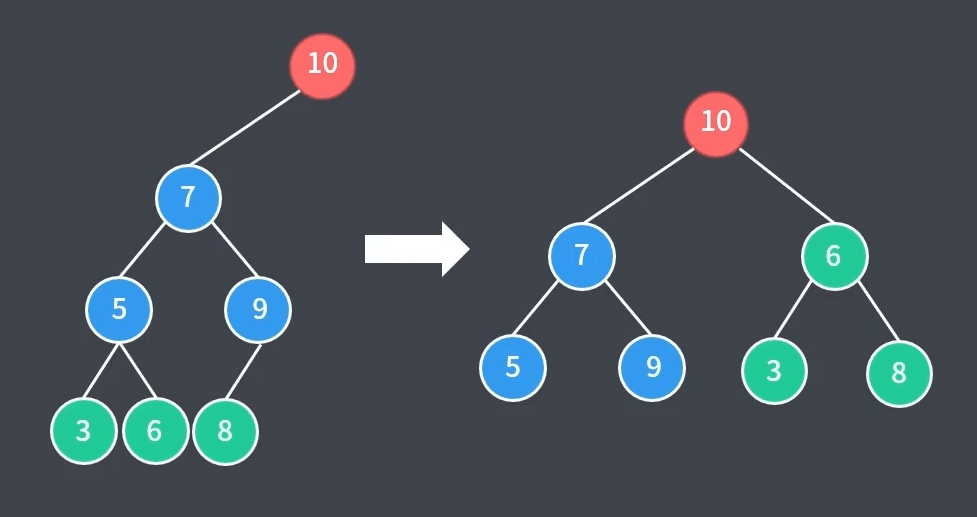
二叉树的性质
1、二叉树第 $i$ 层最多有 $2^{i-1}$ 个节点;高度为 $h$ 的二叉树最多有 $2^h-1$ 个节点(即满二叉树)
2、非空二叉树中,叶子结点个数比二分支节点个数多 $1$ 个。根据下图辅助证明:令度为 $0$、$1$、$2$ 的节点个数分别为 $n_0$、$n_1$、$n_2$,则有 $n = n_0 + n_1 + n_2$ ;此外,由于总节点个数 = 边的个数 $+ 1$ ,则有 $n = 0n_0 + 1n_1 + 2n_2 + 1 = n_1 + 2n_2 + 1$,联立两式证得:$n_0 = n_2 + 1$
3、用 $n$ 个节点构成一棵二叉树,其最小的高度(即构成完全二叉树时的高度)为:$h = log_2(n+1)$ 或 $log_2 n + 1$
二叉树的存储
描述
1、先前介绍过了树的存储结构,二叉树的存储思路也与之类似,分为顺序存储和链式存储
2、顺序存储:思路与前面介绍的相同,使用数组。注意,顺序存储只适用于完全二叉树形式(如果不是完全二叉树,其空缺的节点应留空),节点中存储的父节点和两个子节点的下标应使用先前的关系公式来指代。顺序存储的特点为:存取快、增删慢、仅适用于完全二叉树形式
3、链式存储:与前面介绍的类似,用链表存储,节点中存储父节点和两个子节点的指针。链式存储的特点为:存取慢、增删快。由于便于维护以及拥有更好的普适性,所以我们着重介绍链式存储,其代码如下链式存储代码实现
#include <iostream> #include <memory> using namespace std; // 树的最大节点个数 #define MAX_TREE_SIZE 256 // 树的节点的数据类型 typedef int ElemType; // 树的节点 typedef struct TreeNode { ElemType value; // 存储的数据 shared_ptr<TreeNode> left, right; // 指向左子节点、右子节点 shared_ptr<TreeNode> parent; // 指向父节点 // 构造函数 TreeNode(ElemType val) : value(val), left(nullptr), right(nullptr) { } // 关联节点的成员函数 void LinkNodes(shared_ptr<TreeNode> leftNode, shared_ptr<TreeNode> rightNode, shared_ptr<TreeNode> parentNode) { left = leftNode; right = rightNode; parent = parentNode; } // 释放当前节点的成员函数 void ReleaseNode() { // 不要担心只释放了当前节点的值,由于智能指针的机制,当与该节点有关联的父节点和子节点更换绑定时,该节点的智能指针引用计数将 -1 // 在该节点有关联的节点全部换绑之前,智能指针会保护这些数据不被销毁;当所有有关联的节点全部换绑后,引用计数为 0,数据将自动被销毁 left = nullptr; right = nullptr; parent = nullptr; } } Node; int main() { // 使用 shared_pointer 智能指针,用 make_shared 创建对象 // 也可以用 new 实现,如: Node *root = new Node(1); ,这样的话需要自行更改程序,并确保程序安全 // 创建二叉树:根节点,其默认值为 1 shared_ptr<Node> root = make_shared<Node>(1); // 使用时,创建新的节点,例如现在根节点下有数据为 2 的左子节点,数据为 3 的右子节点 shared_ptr<Node> leftChild = make_shared<Node>(2); shared_ptr<Node> rightChild = make_shared<Node>(3); // 创建后,需要关联对应的节点 root->LinkNodes(leftChild, rightChild, nullptr); leftChild->LinkNodes(nullptr, nullptr, root); rightChild->LinkNodes(nullptr, nullptr, root); // 输出数据 cout << root->value << ' ' << root->left->value << ' ' << root->right->value << endl; // 使用后,销毁节点 leftChild->ReleaseNode(); rightChild->ReleaseNode(); root->ReleaseNode(); /* 注意,这三个节点在当前示例中实际并未被销毁,因为第 47、50、51 行仍有 shared_ptr 指向它们的数据,应将它们指向 nullptr 实际使用中,不会像这样创建根节点,通常只以根节点为标志向下创建子树(root->left = make_shared<Node>(value)),或只需要 root 和一个公用的 child 用于辅助创建节点 如果是这种使用方式,ReleaseNode 就可以自动释放数据了,但仍需要(也只需要)手动设置 root = nullptr 如果可能,最好自行在 Node 的基础上根据需要封装 Tree 类型,以便更方便地使用 */ return 0; }
二叉树的遍历
遍历顺序
1、二叉树有多种遍历顺序,其规则分别如下
2、先序遍历:也称先根遍历,其遍历顺序为根-左-右。下例先序遍历过程为:$10-7-5-3-6-9-8-13-11-12-18$
3、中序遍历:也称中根遍历,其遍历顺序为左-根-右。下例中序遍历过程为:$3-5-6-7-8-9-10-11-12-13-18$
4、后序遍历:也称后根遍历,其遍历顺序为左-右-根。下例后序遍历过程为:$3-6-5-8-9-7-12-11-18-13-10$
5、层次遍历:按照层次顺序进行遍历,同层级按照从左向右的顺序遍历。下例层次遍历过程为:$10-7-13-5-9-11-18-3-6-8-12$
先序遍历代码实现
// 先序遍历(递归) void PreOrder(shared_ptr<Node> root) { // 节点为空,什么都不做 if (root == nullptr) return; // 访问根节点数据 cout << root->value << '-'; // 访问左子树 PreOrder(root->left); // 访问右子树 PreOrder(root->right); } // 先序遍历(循环),伪代码,利用栈的思路实现 void PreOrderByFor(shared_ptr<Node> root) { // 根节点入栈,push 用于实现入栈 push(node); // 循环遍历,isEmptyStack 用于确定栈是否为空 while (!isEmptyStack()) { // cursor 表示当前节点,getTop 用于获取栈顶元素(但不出栈) shared_ptr<Node> cursor = getTop(); // 如果节点不为空 if (cursor != nullptr) { // 访问根节点数据 cout << cursor->value << '-'; // 将当前根节点的左子树入栈 push(cursor->left); } // 如果节点为空,说明当前元素无效,出栈 else { // 10-7-5-3-3.left // pop 用于获取栈顶元素(并出栈),弹出栈顶空的无效元素 pop(); // 10-7-5-3 // 当前栈顶元素已经完成了根-左的访问,接下来只需要访问右子树。根节点出栈,其右子树进栈 cursor = pop(); push(cursor->right); } } }中、后序遍历代码实现
// 只需在先序遍历的基础上稍作修改即可 // 中序遍历(递归) void InOrder(shared_ptr<Node> root) { // 节点为空,什么都不做 if (root == nullptr) return; // 访问左子树 InOrder(root->left); // 访问根节点数据 cout << root->value << '-'; // 访问右子树 InOrder(root->right); } // 后序遍历(递归) void PostOrder(shared_ptr<Node> root) { // 节点为空,什么都不做 if (root == nullptr) return; // 访问左子树 PostOrder(root->left); // 访问右子树 PostOrder(root->right); // 访问根节点数据 cout << root->value << '-'; }层次遍历代码实现
1、层次遍历的一个问题是如何实现按层遍历,由于树是链式的,很难在遍历完树的最右侧节点后找到下一层的最左侧节点
2、一种解决办法是使用队列来按层处理,每次按顺序进入一层的节点,再在队列中访问下一层节点。此时前一层节点离开队列,新一层节点进入队列// 队列:临时存储上一层节点;层次遍历的顺序与进入/离开队列的顺序一致 // 也可以使用顺序结构(数组)实现队列,但链式结构更加灵活 typedef struct LinkedNode { shared_ptr<Node> node; // 存储队列当前元素 shared_ptr<LinkedNode> next; // 指向队列下一个元素 // 构造函数 LinkedNode(shared_ptr<Node> n) : node(n), next(nullptr) { } } Queue; // 定义队列的(虚拟的)首节点和尾节点 shared_ptr<Queue> head, tail; // 初始化队列 shared_ptr<Queue> initQueue() { shared_ptr<Node> temp = make_shared<Node>(-1); // 构造具有(树中数据)非法值的节点(该节点数据实际不使用) head = make_shared<Queue>(temp); tail = head; return head; } // 判断队列是否为空 bool isEmpty() { if (head == tail) return true; return false; } // 将节点计入队列末尾 void push(shared_ptr<Node> node) { shared_ptr<Queue> _next = make_shared<Queue>(node); // 创建队列新节点 tail->next = _next; // 将其挂载到队列末尾 tail = _next; // 将队列末尾指向新节点 } // 获取队列的头部(并退出队列) shared_ptr<Queue> pull() { if (isEmpty()) return nullptr; shared_ptr<Queue> first = head->next; // 获取第一个有效节点(注意不是 head,是 head 的下一个节点) head->next = first->next; // 将队列首节点指向下一个(第二个)有效节点 // 如果没有后续节点,将 tail 设置指向 head if (first->next == nullptr) tail = head; // 将 first 与队列下一个节点断开 first->next = nullptr; return first; } // 层次遍历 void LevelOrder(shared_ptr<Node> node) { // 初始化辅助队列 initQueue(); // 将树的根节点入队 push(node); // 循环将每个层次的节点入队出队 while (!isEmpty()) { // 将队列的第一个有效节点出队 shared_ptr<Queue> queueNode = pull(); // 访问节点数据 shared_ptr<Node> treeNode = queueNode->node; cout << treeNode->value << '-'; // 将节点的左右孩子入队 if (treeNode->left != nullptr) push(treeNode->left); if (treeNode->right != nullptr) push(treeNode->right); } }
线索二叉树
线索二叉树
1、在先前的遍历实现中,本质上都是使用了递归(栈 + 循环)的实现方式,而其中的栈会额外占用内存,而线索二叉树便是用来改进这一缺陷的
2、线索二叉树:利用空的链表节点存储节点的父节点和子节点,以加快查找速度。其还需要两个标志,表明指向的是孩子节点还是线索
3、线索二叉树的构建是在前/中/后序遍历中完成的(其指向的线索就是当前节点在当前遍历方式中上/下一个要遍历的节点),数据结构实现如下typedef struct ThreadTreeNode { ElemType value; // 存储的数据 bool lTag = false, rTag = false; // 为 true 表示 left/right 指向线索,为 false 表示指向子节点 // 当前节点如果有左/右子节点,则指向左/右子节点,否则指向线索 // left 指向遍历中上一个遍历的节点,right 指向遍历中下一个遍历的节点 shared_ptr<ThreadTreeNode> left, right; // 构造函数 ThreadTreeNode(ElemType val) : value(val), left(nullptr), right(nullptr) { } } Node;前序遍历
1、构造前序线索二叉树:通过前序遍历使二叉树线索化,如下图前序遍历(根-左-右)为 $10-7-5-9-8-14-12-11-13-18$,前序线索二叉树代码实现如下
2、大致思路为:定义preNode记录前序遍历过程中上次访问的节点;在遍历过程中,如果当前节点没有左子节点,则设置左指针指向preNode;再检查如果前一个节点没有右子节点,则设置preNode->right指向当前节点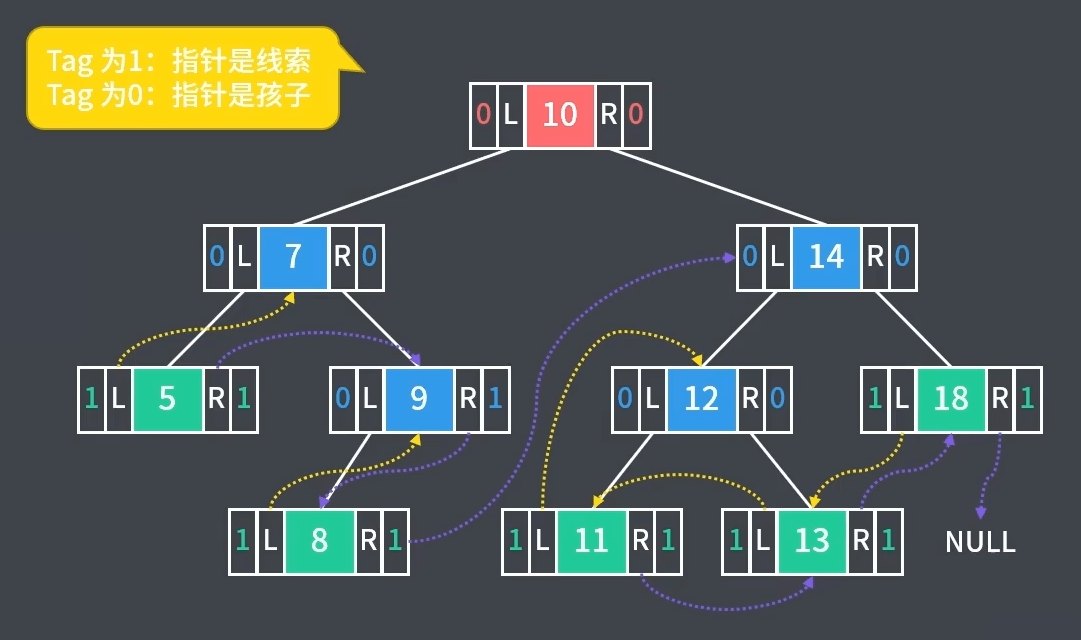
shared_ptr<Node> preNode = nullptr; // 记录遍历过程中的前一个节点 // 前序遍历:线索化二叉树 void PreOrderThread(shared_ptr<Node> root) { // 节点为空,什么都不做 if (root == nullptr) return; // 检查并设置当前节点的左线索 if (root->left == nullptr) { root->left = preNode; root->lTag = true; } // 检查并设置前一个节点的右线索 if (preNode != nullptr && preNode->right == nullptr) { preNode->right = root; preNode->rTag = true; } // 设置当前节点为前一个节点 preNode = root; // 由于先前(或递归归来时) left/right 可能被设置了线索,所以需要判断是否被设置过 // 访问左子树 if (!root->lTag) PreOrderThread(root->left); // 访问右子树 if (!root->rTag) PreOrderThread(root->right); } // 创建前序线索二叉树 void CreatePreOrderThread(shared_ptr<Node> root) { if (root != nullptr) { preNode = nullptr; // 初始化 preNode PreOrderThread(root); // 通过前序遍历线索化二叉树 // 设置最后一个节点的右线索 if (preNode != nullptr) { preNode->right = nullptr; preNode->rTag = true; } } } // 前序遍历二叉树,因为有线索存在,所以二叉树可以链式访问 void PreOrderByFor(shared_ptr<Node> root) { shared_ptr<Node> cursor = root; while (cursor != nullptr) { cout << cursor->value << '-'; // 前序遍历,如果有左子节点,向 left 访问子节点,否则向 right 访问线索 if (!cursor->lTag) cursor = cursor->left; else cursor = cursor->right; } }中序遍历
1、构造中序线索二叉树:通过中序遍历使二叉树线索化,如下图中序遍历(左-根-右)为 $5-7-8-9-10-11-12-13-14-18$,中序线索二叉树代码实现如下
2、实现思路与前序线索二叉树类似,代码在其基础上稍作修改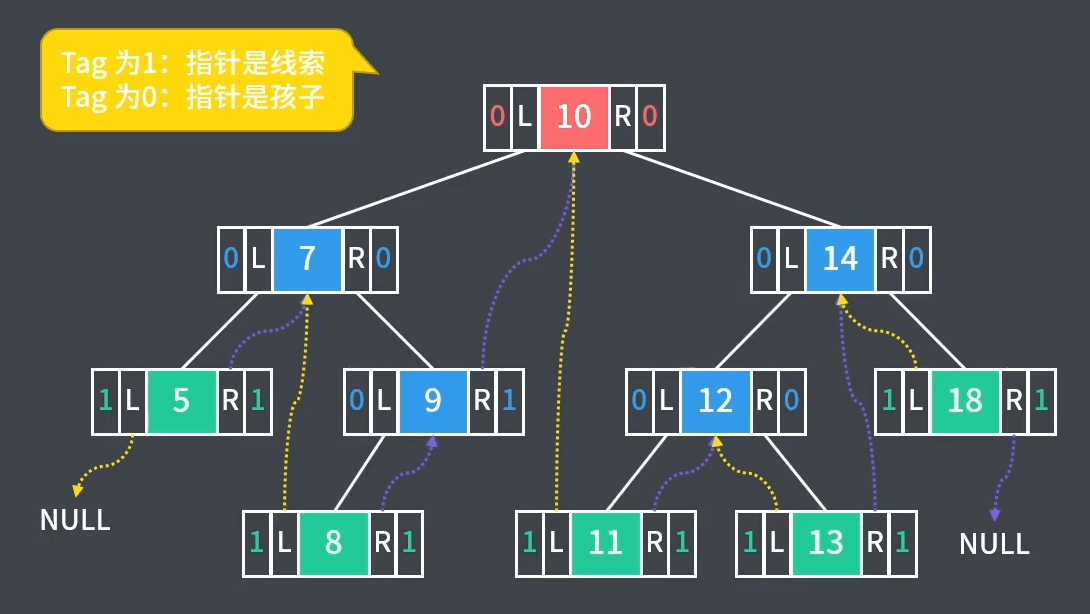
shared_ptr<Node> preNode = nullptr; // 记录遍历过程中的前一个节点 // 中序遍历:线索化二叉树 void InOrderThread(shared_ptr<Node> root) { // 节点为空,什么都不做 if (root == nullptr) return; // 访问左子树 InOrderThread(root->left); // 检查并设置当前节点的左线索 if (root->left == nullptr) { root->left = preNode; root->lTag = true; } // 检查并设置前一个节点的右线索 if (preNode != nullptr && preNode->right == nullptr) { preNode->right = root; preNode->rTag = true; } // 设置当前节点为前一个节点 preNode = root; // 访问右子树 InOrderThread(root->right); } // 创建中序线索二叉树 void CreateInOrderThread(shared_ptr<Node> root) { if (root != nullptr) { preNode = nullptr; // 初始化 preNode InOrderThread(root); // 通过前序遍历线索化二叉树 // 设置最后一个节点的右线索 if (preNode != nullptr) { preNode->right = nullptr; preNode->rTag = true; } } } // 中序遍历二叉树,因为有线索存在,所以二叉树可以链式访问 void InOrderByFor(shared_ptr<Node> root) { if (root == nullptr) return; shared_ptr<Node> cursor = root; // 获取第一个遍历的节点(最左侧节点),该节点的 lTag 为 true while (!cursor->lTag) cursor = cursor->left; while (cursor != nullptr) { cout << cursor->value << '-'; // 中序遍历,如果有右子节点,向 right 访问子节点,否则向 right 访问线索 if (!cursor->lTag) { cursor = cursor->right; // 此时 cursor 可能是有左子树的,应先访问左子树 // 获取左子树第一个节点,该节点的 lTag 为 true while (!cursor->lTag) cursor = cursor->left; } else cursor = cursor->right; } }后序遍历
1、构造后序线索二叉树:通过后序遍历使二叉树线索化,如下图后序遍历(左-右-根)为 $5-8-9-7-11-13-12-18-14-10$
2、实现思路与前序线索二叉树类似,代码在其基础上稍作修改,此处省略具体代码实现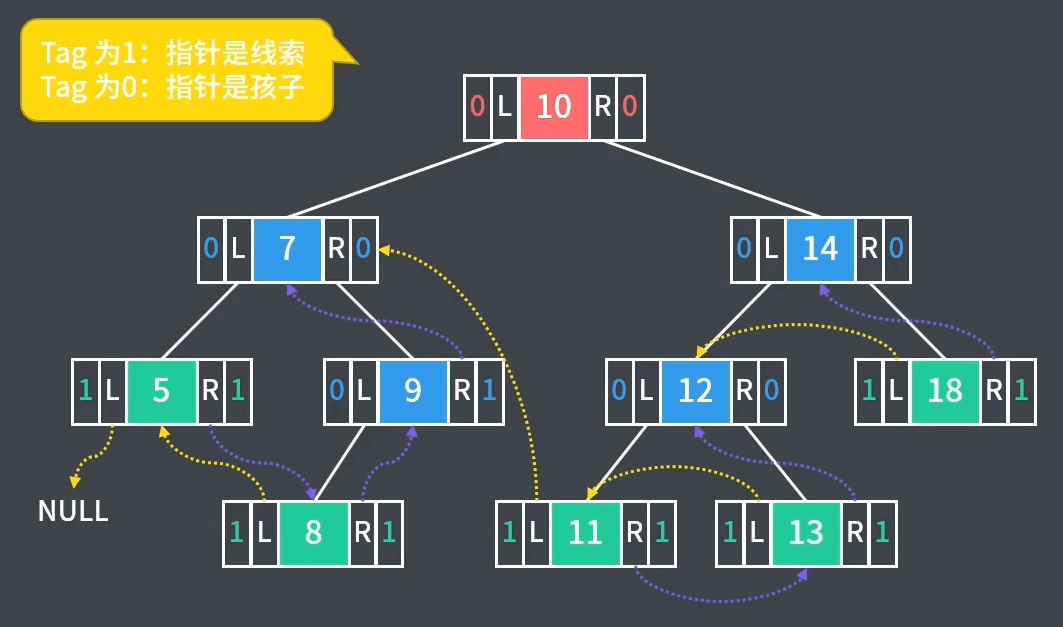
简易技巧
从树快速得到遍历
1、已知一棵二叉树,快速得到其遍历序列有一个简单的方法,如下图(绿色为前序,红色为中序,蓝色为后序)
2、先序遍历:在二叉树图上每个节点左侧画一个圈,从根节点开始向左逆时针绕着二叉树的枝画线,按顺序穿过所画的圈,这个顺序便是先序遍历
3、中序遍历在每个节点下方画一个圈,后序遍历在在每个节点右侧画一个圈,其余步骤相同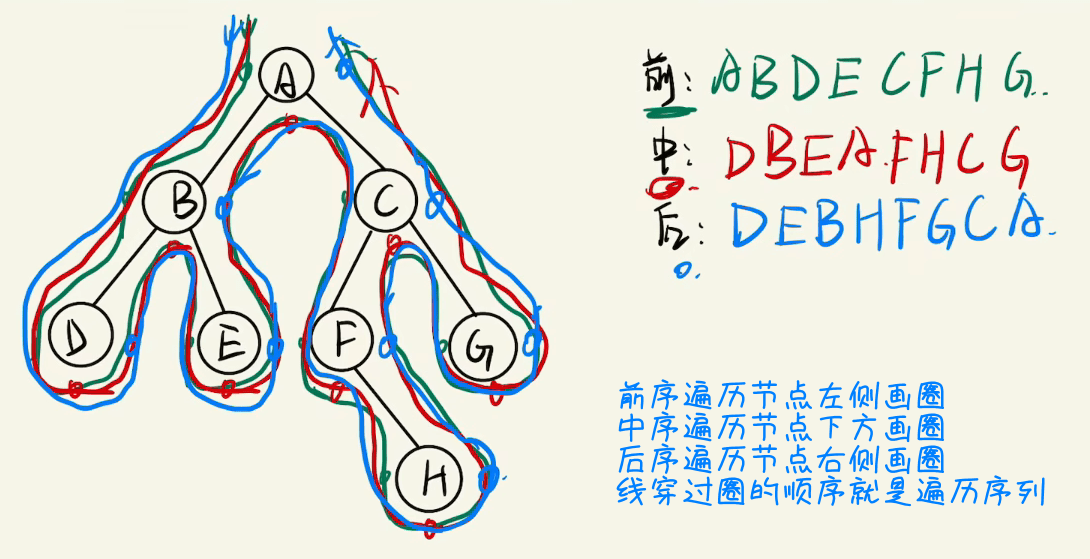
从遍历推导树
1、至少要已知中序遍历+另一种遍历才能推导出唯一的树。注意,前序遍历+后序遍历不能确定唯一的树
2、有一种较为简单的推导方式,其将中序遍历的序列在横轴自左向右排列,先序遍历的序列在纵轴自上而下排列,后序遍历的序列在纵轴自下而上排列,对应字母落在方格图的对应位置。具体原理和使用方法如下图
3、注意:树的关系连接需要遵循这些规则。从先/后序遍历中确定根元素,即按规则排列的纵轴的第一个元素是根;横轴中序遍历的序列中,任意元素的左侧元素一定是该父节点的左子树中元素,反之,任意元素的右侧元素一定是该父节点的右子树中元素(注意,父子节点的连接不是直接根据自上而下连接的,还需要结合该条关系)



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试