图的存储
邻接表
1、在计算机中,图的存储方式有多种,最常用的是邻接表和邻接矩阵。邻接矩阵由于适用范围很小,故一般不考虑这种写法
2、出度:如下图便是一幅有向图,其中一个节点指向的其他节点称为这个节点的出度,指向出度节点的路径称为这个节点的出边。如下图中 $2$、$5$ 为 $1$ 的出度
3、邻接表:就是将一个点的所有出点(邻接点)保存在一个数组中;拓展的过程,也就是遍历这个数组的过程。这个数组我们称为邻接表
vector 邻接表建图
1、上述数组的长度显然是可变的,所以选择使用
vector来建图
2、我们将每个点的所有出点存入对应的vector中,命名为 $g[]$ (graph)
3、拓展的时候,只需要遍历对应的 $g[]$ 数组即可,且vector建图的出点支持排序邻接矩阵
1、简言之,是一个二维数组,其第一维的索引表示入点,第二维的索引表示出点,$g[i][j]$ 表示 $i$ 到 $j$ 的权值
2、由于通常邻接矩阵难以处理数据,且会浪费大量空间,所以通常不考虑用它建图
图的遍历
DFS 深度优先搜索
1、DFS是深度优先搜索,英文为Depth First Search。一句话简言之:一条路走到黑
2、其算法精髓是先往深处走,走完了再回头
3、对应的数据结构是栈,每次从栈顶取出一个点,再将所有出点入栈,完成一次拓展// 深度优先(可用递归,也可用栈实现) void DFS(int x) { cout << g[x] << ' '; // 输出当前节点 // 深度优先,遍历当前节点所有出点 for (int &y : g[x]) { if (该元素先前已被遍历过) continue; DFS(y); // 深度优先地向下递归 } }BFS 广度优先搜索
1、BFS是广度优先搜索,英文为Breadth First Search。与 DFS 不同,其每次将所有出点放入队列,然后小心地向下试探
2、其算法精髓是小步走,尽量不往深处走
3、对应的数据结构是队列,每次从队头取出一个点,然后将所有出点推入队列,完成一次拓展// 广度优先(用队列实现) void BFS(int root) { queue<int> q; // 创建队列 q.push(root); // 将初始节点推入队列 // 只要队列不为空 while (q.size()) { int x = q.front(); // x 获取队头 q.pop(); // 释放队头 cout << x << ' '; // 输出当前节点 for (auto &y : g[x]) { if (该元素先前已被遍历过) continue; q.push(y); // 将出点推入队尾 } } }补充说明
1、以上两种搜索一般都需要保证不走重复的点,否则很容易产生环从而无限循环,所以会使用一个
bool vis[]来标记某个点是否走过。但是树上一般不需要标记,因为树一定没有环
2、一般来说,DFS 用来求树上问题较多,BFS 用于求权值相等的最短路(最少操作次数等)
例-树的遍历
树的遍历
1、树的遍历:给定一棵大小为 $n$($n \leq 50$),根为 $1$ 的树,求出其按照DFS和BFS进行遍历时的顺序,将所有出点按照编号从小到大排序后进行遍历。输入一个整数 $n$ 表示树的大小,接下来 $n-1$ 个整数表示 $2 \to n$ 的父节点。第一行输出 DFS 序,第二行输出 BFS 序
2、存储树最简单的办法就是存储节点的父节点,只要知道树的根节点和每个节点的父节点就可以表示一棵树。我们可以反过来,用图存储父节点的子节点(出度),再对图进行BFS和DFS遍历即可
3、由于树上的元素遍历时不会重复,不会形成环,所以不需要打标记确定重复代码实现
#include <bits/stdc++.h> using namespace std; const int N = 60; vector<int> g[N]; // 图 int fa[N]; // 二叉树节点的父节点 // 深度优先(也可以通过 stack 实现) void DFS(int x) { cout << x << ' '; // 输出当前节点 // 遍历当前节点的所有出点 for (auto &y : g[x]) { // 如果 y 作为 x 的出点指向了 x 的父节点,则跳过(针对双向图,该题可以省略) if (y == fa[x]) continue; DFS(y); // 递归地向下遍历 } } // 广度优先 void BFS(int root) { queue<int> q; // 创建队列 q.push(root); // 将初始节点推入队列 // 只要队列不为空 while (q.size()) { int x = q.front(); // x 获取队头 q.pop(); // 释放队头 cout << x << ' '; // 输出当前节点 for (auto &y : g[x]) { // 如果 y 作为 x 的出点指向了 x 的父节点,则跳过(针对双向图,该题可以省略) if (y == fa[x]) continue; q.push(y); // 将出点推入队尾 } } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; for (int i = 2; i <= n; i++) { cin >> fa[i]; // 输入 i 的父节点 g[fa[i]].push_back(i); // 建立图,从父节点 fa[i] 指向子节点 i } // 对出点进行排序 for (int i = 1; i <= n; i++) sort(g[i].begin(), g[i].end()); DFS(1); cout << endl; BFS(1); cout << endl; return 0; }
例-图的遍历
图的遍历
1、图的遍历:给定一个 $n$ 个点 $m$ 条边的有向图,图中可能有重边和自环,点的编号为 $1 \to n$ 。求出从点 $1$ 出发,能够到达的所有点,升序输出
2、由于可能出现闭环,所以需要防止重复,使用 $vis[i]$ 记录点 $i$ 有没有被走过即可代码实现
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 10; vector<int> g[N]; bitset<N> vis; // 默认为 0 void DFS(int x) { // 如果走过该节点,就跳过 if (vis[x]) return; vis[x] = true; for (auto &y : g[x]) DFS(y); } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n, m; cin >> n >> m; while (m--) { int u, v; cin >> u >> v; // 效果同 u != v,防止自环 if (u ^ v) g[u].push_back(v); } DFS(1); // 此时 vis[] 已记录了走过的点,运用桶排序思想,升序输出 for (int i = 1; i <= n; i++) if (vis[i]) cout << i << ' '; return 0; }
回溯与剪枝
回溯法模板(基于 DFS)
func() { 递归出口; 剪枝函数; 向后拓展(可能还包含剪枝) { 修改现场; func(); 恢复现场; } }回溯法特点
解决一切问题
1、用回溯法几乎可以解决所有问题,但只能在问题规模较小时使用
2、当问题规模较大时基本就失效了,因为时间复杂度极高生成解空间
1、回溯法可以用于生成解空间,其实就是一个带剪枝的暴力枚举
2、回溯法通常用于生成子集树、排列树等解空间,然后在解空间中通过数学方法来剪枝,即减少不必要的操作,从而缩小解空间。最终找出最好的解往回走恢复现场
1、回溯法之所以叫回溯,是因为所有子问题的解最终都要回归到原问题。通过合并操作,利用函数关系进行解的传递
2、恢复现场是及其关键的一步,常见的恢复现场包括对标记的恢复、数组状态的恢复、局面地图的恢复等
例-全排列
全排列
1、全排列:给定数字 $n$,按字典序输出排列 $[1, 2, \ldots, n]$ 的全排列
2、如下图,演示使用树状图思想构造全排列,对该树进行DFS即可得到一种排列。所以我们可以通过回溯构造这样的树
3、注意,过程中应使用 $vis[]$ 记录该数字是否被选择过,剪枝减少重复,否则复杂度为 $O(n^n)$,剪枝后可使复杂度降为 $O(n!)$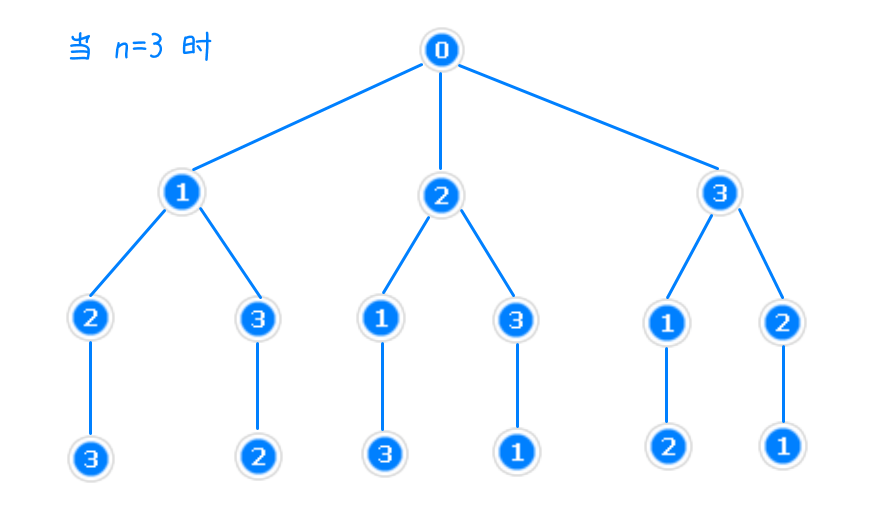
代码实现
#include <bits/stdc++.h> using namespace std; const int N = 15; int a[N], n; bitset<N> vis; // dep 表示当前深度 void DFS(int dep) { // 如果深度足够了,表示 a[1 ~ n] 都确定了 if (dep == n + 1) { for (int i = 1; i <= n; i++) cout << a[i] << " \n"[i == n]; return; } // 遍历选择这一层的 a[dep] 的值 for (int i = 1; i <= n; i++) { // 剪枝:如果之前出现过 i,就跳过 if (vis[i]) continue; // 修改状态 a[dep] = i; // 当前层 a[dep] 征用了 i vis[i] = true; // 记录 i 被征用 DFS(dep + 1); // 向下枚举 // 回溯:恢复现场 vis[i] = false; a[dep] = 0; } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); cin >> n; DFS(1); return 0; }
例-N 皇后
N 皇后
1、N 皇后:现在有一个 $n \times n$ 的棋盘,要放入 $n$ 个皇后,要满足每个皇后的攻击范围(横竖斜)内不能出现其他皇后,找出所有的可行方案
2、我们将棋盘每一行看作一层,易知每一层有且只有一个皇后。按照层次进行枚举,例如第一层选择 $(0, 0)$ 位置,此时修改棋盘的状态,标记其攻击范围为不可落子状态,再进行第二层的落子。如果到某一层发现无法落子(如下图),那么就必须向上一层回溯,要将上一层设置的状态解除,并重新向下枚举上一层的落点,再继续向下尝试。如果所有层都可以落子,表明这是一种合法的方案
3、接下来处理如何标记被占领状态。我们可以发现,每一层(第 $i$ 层)只需要枚举不需要标记,每一列可以用 $vis[j]$ 表示第 $j$ 列被占;此时可以用 $vis2[k]$ 表示 $i + j = k$ 这条左下-右上的斜线被占,可以用 $vis3[k]$ 表示 $i + n - j = k$ 这条左上-右下的斜线被占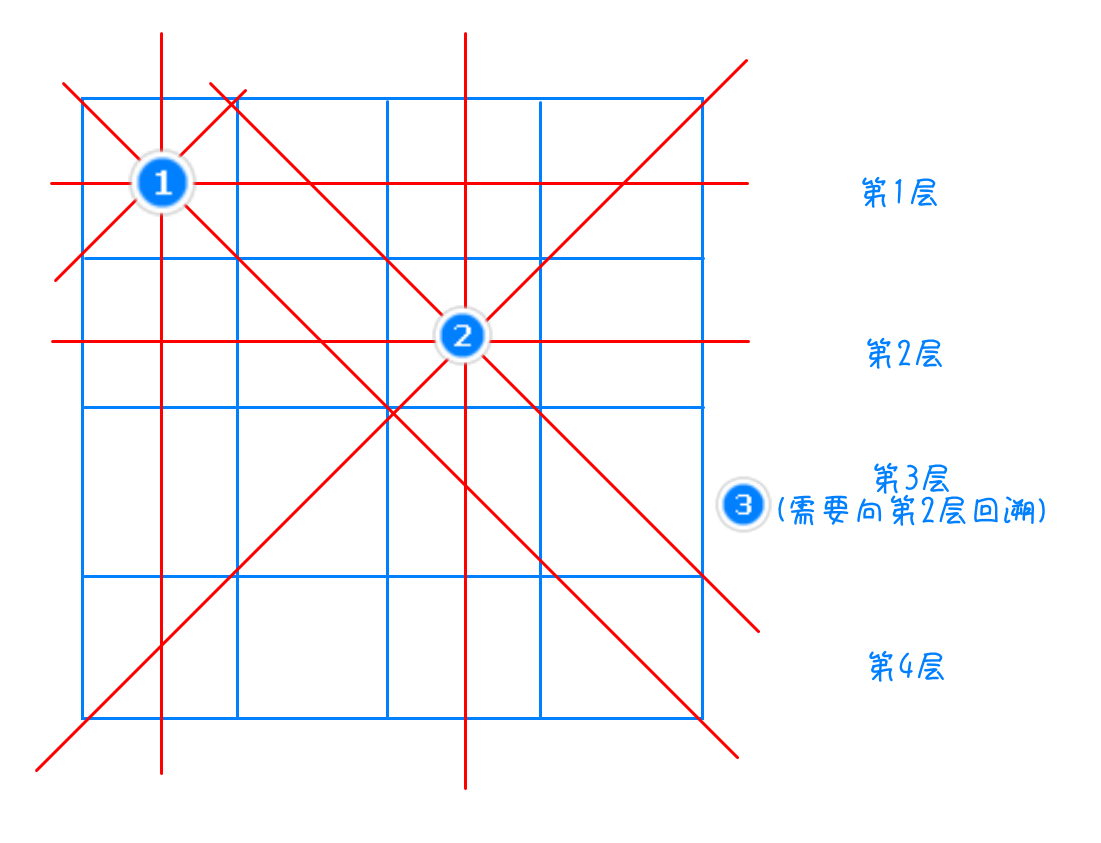
代码实现
#include <bits/stdc++.h> using namespace std; const int N = 15; vector<vector<string>> res; // 返回的结果 vector<string> tmp; // 当前状态的地图情况 bitset<N> vis, vis2, vis3; // true 表示被占领 // 表示当前正在处理第 dep 行 void DFS(int dep, int n) { // 递归出口 if (dep == n) { // 执行此处时,说明已经完成了合法的地图,将其计入答案 res.push_back(tmp); return; // 退出 } // 向后拓展:第 dep 行,选择第 j 个位置落子 for (int j = 0; j < n; j++) { // 判断可行性,剪枝(也可单独写一个剪枝函数) if (vis[j] || vis2[dep + j] || vis3[dep + n - j]) continue; // 修改现场(状态转移) vis[j] = true; vis2[dep + j] = true; vis3[dep + n - j] = true; tmp[dep][j] = 'Q'; // 继续处理下一行 DFS(dep + 1, n); // 恢复现场 vis[j] = false; vis2[dep + j] = false; vis3[dep + n - j] = false; tmp[dep][j] = '.'; } } int main() { int n; cin >> n; tmp.resize(n); // 初始化为 n 的大小 for (int i = 0; i < n; i++) { tmp[i].resize(n); // 每一行的字符串也初始化为 n 的大小 for (int j = 0; j < tmp[i].size(); j++) tmp[i][j] = '.'; // 将整个地图初始化为 . } DFS(0, n); // 输出答案 for (auto ans : res) { for (int i = 0; i < n; i++) cout << ans[i] << endl; cout << endl; } return 0; }
无权最短路
小 e 走迷宫
1、小 e 走迷宫:给定大小为 $n \times m$ 的矩阵迷宫,矩阵中 $0$ 表示空白,$1$ 表示障碍。起始点位于最左上角 $(1, 1)$ 处,终点在最右下角 $(n, m)$ 处,每秒可以向任意方向移动。输出所需最短时间,如果不能到达输出 $-1$
2、题目实际是求无权最短路,不可以用 DFS 实现,错误思路如后附。该思路正确所需的注意点有:判断下一步不要出界;判断 $vis[i]$ 没有走过防止重复;更新 $d[next\_x][next\_y]$ 时,可能先前已经有寻过更短的 $d[next\_x][next\_y]$ ,不要直接用 $d[i][j] + 1$ 覆盖,要取二者最小值。该思路的根本错误点在:标记 $vis[i]$ 后,之后寻其他路时会被 $vis$ 错误阻挡;而如果不标记或者回溯 $vis[i]$ ,会形成闭环死循环
3、因此,应当用 BFS 实现。BFS 会一层一层向外拓展,每层拓展到的点都是当前的最短路(且相等),这其实也是一种贪心的思想。该思路除了 DFS 需要的注意点,还需注意:不要在while从队列取出点时才标记 $vis[i]$ ,应当在先前向队列push该点时就标记,否则同一层中再次遍历到该点会重复入队;BFS 更新 $d[next\_x][next\_y]$ 时不需要取最小值,因为同一层能到达 $(next\_x, next\_y)$ 的距离都是最短且相等的正确实现:BFS
#include <bits/stdc++.h> using namespace std; const int N = 1e3 + 10, INF = 0x3f; int n, m; int mp[N][N]; // 原地图 int d[N][N]; // d[i][j] 表示从 (1,1) 到 (i,j) 的最短时间(最短距离) bitset<N> vis[N]; // 标记点是否走过 // 用于控制点的移动 int dx[] = {0, 0, 1, -1}; // x 方向(行方向,上下)的偏移量 int dy[] = {1, -1, 0, 0}; // y 方向(列方向,左右)的偏移量 // 判断该点是否在地图范围内 bool in_map(int x, int y) { return 1 <= x && x <= n && 1 <= y && y <= m; } // 求无权最短路 // 广度优先会沿着 0 一层一层向外走,所以每一层向外能走到的点都是当前离 (1, 1) 距离相同且最近的点 void BFS(int x, int y) { queue<pair<int, int>> q; q.push({x, y}); vis[x][y] = true; while (q.size()) { int x = q.front().first, y = q.front().second; q.pop(); // 枚举下一步的偏移量 for (int i = 0; i < 4; i++) { // 枚举下一步的坐标,顺序为 右->左->下->上 int next_x = x + dx[i], next_y = y + dy[i]; // 防止走到下标 0 的边界,如果在地图内 且 没有障碍 且 没有走过 if (in_map(next_x, next_y) && !mp[next_x][next_y] && !vis[next_x][next_y]) { // 由于 BFS 一层一层向外拓展,所以能到达 (next_x, next_y) 的点中 d[x][y] + 1 一定是最近距离 d[next_x][next_y] = d[x][y] + 1; q.push({next_x, next_y}); // 广度优先,将下一个点放入队列 vis[next_x][next_y] = true; // 标识已经入队,防止同一层内重复入队 } } } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); cin >> n >> m; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) cin >> mp[i][j]; BFS(1, 1); // 如果不能走到 (n, m) if (!vis[n][m]) cout << "-1"; else cout << d[n][m]; return 0; }错误实现:DFS
// 错误思路:DFS /* 错误样例 5 6 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 1 0 */ #include <bits/stdc++.h> using namespace std; const int N = 1e3 + 10, INF = 0x3f; int n, m; int mp[N][N]; // 原地图 int d[N][N]; // d[i][j] 表示从 (1,1) 到 (i,j) 的最短时间(最短距离) bitset<N> vis[N]; // 标记点是否走过 int dx[] = {0, 0, 1, -1}; // x 方向(行方向,上下)的偏移量 int dy[] = {1, -1, 0, 0}; // y 方向(列方向,左右)的偏移量 // 判断该点是否在地图范围内 bool in_map(int x, int y) { return 1 <= x && x <= n && 1 <= y && y <= m; } void DFS(int x, int y) { vis[x][y] = true; // 标记当前点走过 // 枚举下一步的偏移量 for (int i = 0; i < 4; i++) { // 枚举下一步的坐标,顺序为 右->左->下->上 int next_x = x + dx[i], next_y = y + dy[i]; // 防止走到下标 0 的边界,如果在地图内 且 没有障碍 且 没有走过 if (in_map(next_x, next_y) && !mp[next_x][next_y] && !vis[next_x][next_y]) { // 下一步的 d[next_x][next_y] 可能是到当前 d[x][y] 的最短时间 + 1 // 也可能是先前寻路过已有结果的 d[next_x][next_y],取最小值 d[next_x][next_y] = min(d[x][y] + 1, d[next_x][next_y]); DFS(next_x, next_y); } } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); cin >> n >> m; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) cin >> mp[i][j]; memset(d, INF, sizeof(d)); // 初始化 d[] 为无穷 d[1][1] = 0; // 初始化 d[1][1] 为 0 DFS(1, 1); // 如果不能走到 (n, m) if (!vis[n][m]) cout << "-1"; else cout << d[n][m]; return 0; }



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试