重链剖分
重链
1、重儿子:一个节点的最重的儿子,即 size 最大(子树大小最大)的儿子。一个节点至多有一个重儿子,其余都是轻儿子
2、重链:从某个节点开始,一直走重儿子得到的一条链,称为重链。一张图中可能有多条重链,树上的一条简单路径,至多经过 $\log n$ 条重链
3、链顶(顶):一条重链中深度最小的节点,称为链顶,通常直接称为顶
4、如下图,图中节点旁的数字表示节点的 size,标记红色点为顶,红色边连接的路径为一条重链,单独的顶也是一条重链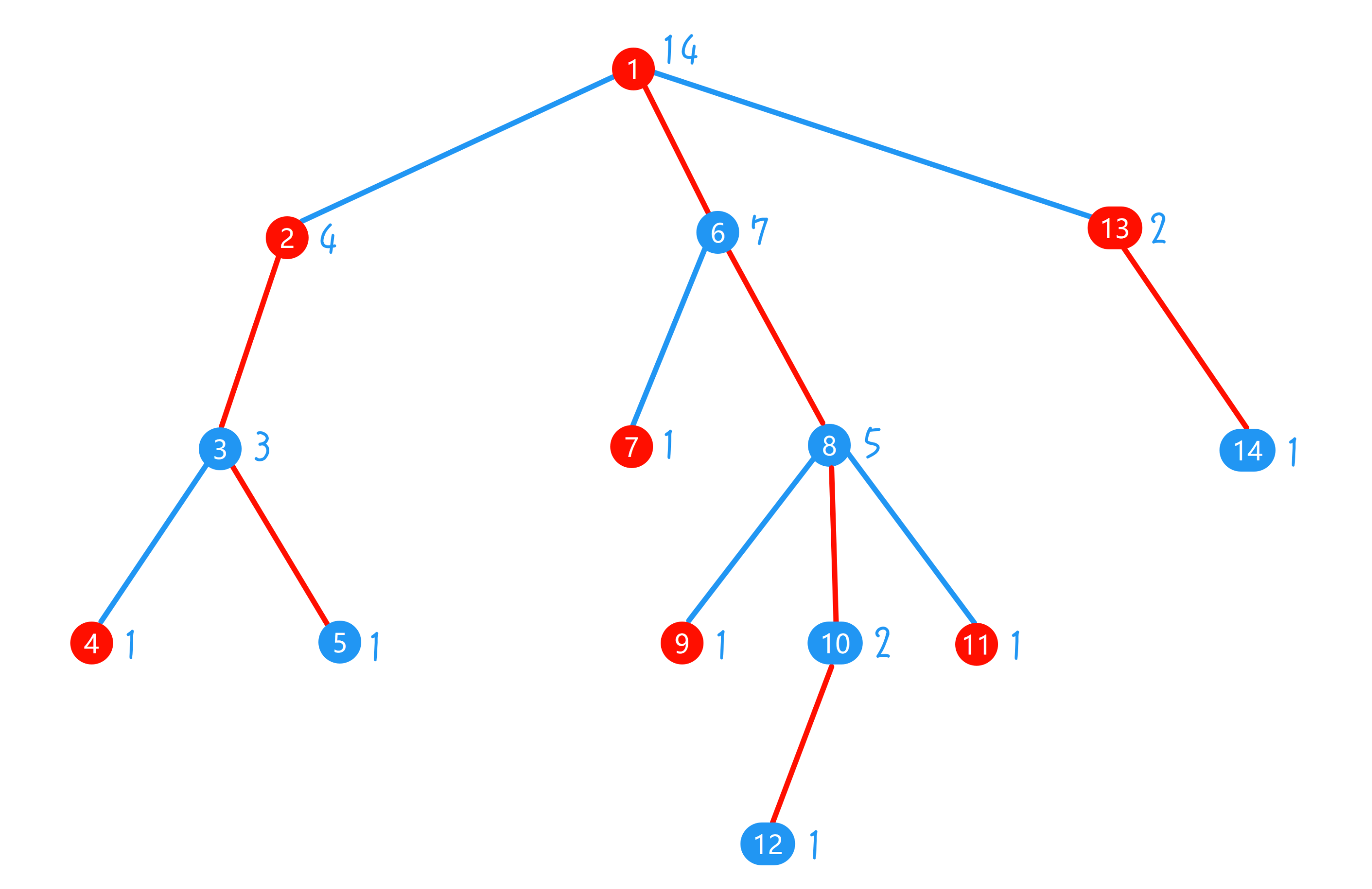
重链剖分
1、将一张图划分为多条重链,称为重链剖分。观察上图,用 $son[]$ 标记每个节点的重儿子,如 $son[1] = 6$;用 $top[]$ 标记每个节点所属重链的顶,如 $top[1,6,8,10,12] = 1$,这样做的目的是可以迅速找到链顶并跳跃到其他链
2、要进行重链剖分,实际就是求 $son[]$ 和 $top[]$。实际实现时,首先跑第一遍 DFS,递归地处理出每个节点的 size,可以顺便求出 $son[]$,再跑第二遍 DFS,递归地处理 $top[]$
3、对于第二次 DFS,多使用一个参数 $t$ 传递链顶。先走重儿子 $son[x]$(需要先判断是否存在),此时传递 $t = t$,即 $son[x]$ 与 $x$ 链顶相同;之后遍历走轻儿子 $y$,传递 $t = y$,即 $y$ 为一条新的重链的链顶。具体模板实现如下,具体应用见例题模板实现
vector<int> g[N]; int sz[N], son[N], top[N]; // 处理 size[] 和 son[] void DFS1(int x) { // 先将每个新点自己的大小标记为 1 sz[x] = 1; // 遍历子节点 for (auto &y : g[x]) { DFS1(y); // 递回时,加上子节点子树的大小 sz[x] += sz[y]; // 如果当前子节点 size 最大,标记为 x 的重儿子 if (sz[y] > sz[son[x]]) son[x] = y; } } // 处理 top[],参数 t 传递链顶 void DFS2(int x, int t) { // 标记 top[] top[x] = t; // 对于重儿子,son[x] 链顶与 x 相同 if (son[x]) DFS2(son[x], t); // 遍历所有轻儿子,轻儿子为新的重链链顶 for (auto &y : g[x]) if (y != son[x]) DFS2(y, y); }
例-重链剖分 LCA
重链剖分 LCA
1、LCA:输入树的节点个数 $n$,这棵树以节点 $1$ 为根,接下来 $n-1$ 行,分别输入节点 $2 \to n$ 的父节点,再输入询问次数 $q$,每个询问给出两个整数 $u, v$,输出 $u, v$ 的最近公共祖先 $lca(u,v)$
2、以求下图 $lca(5, 11)$ 为例,假设图已按照上述方式进行重链剖分。两个点如果在同一条链上,那么深度较小的点即为 $lca$;只要不在一条链上,就将 $top$ 较深的向上跳,因为此时我们将点的问题转换成了链的问题,则应该关注链顶的位置,直到两点位于同一条链上
3、对于每次跳跃,链顶的父亲一定位于一条新的链上,便跳跃到链顶的父亲到达新的链。由于任意一条简单路径经过的重链数最多为 $\log n$,所以跳跃次数不会超过 $\log n$ 次。对于该问题,需要额外的 $fa[]$ 和 $dep[]$ 数组存储父节点和深度
4、该例为重链剖分优化复杂度的一个简单示例,后续例子将学习重链剖分的更高级更常用的应用
代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; vector<int> g[N]; int fa[N], dep[N]; // 父节点和深度 int sz[N], son[N], top[N]; // 重链剖分 // 处理 size[] 和 son[],额外处理 dep[] void DFS1(int x, int pre) { // 先将每个新点自己的大小标记为 1 sz[x] = 1; // 处理深度 pre dep[x] = dep[pre] + 1; // 遍历子节点 for (auto &y : g[x]) { DFS1(y, x); // 递回时,加上子节点子树的大小 sz[x] += sz[y]; // 如果当前子节点 size 最大,标记为 x 的重儿子 if (sz[y] > sz[son[x]]) son[x] = y; } } // 处理 top[],参数 t 传递链顶 void DFS2(int x, int t) { // 标记 top[] top[x] = t; // 对于重儿子,son[x] 链顶与 x 相同 if (son[x]) DFS2(son[x], t); // 遍历所有轻儿子,轻儿子为新的重链链顶 for (auto &y : g[x]) if (y != son[x]) DFS2(y, y); } // 求 LCA int LCA(int x, int y) { // 只要不在同一条链上 while (top[x] != top[y]) { // 将链顶 top 低的向上跳,跳至链顶父节点 if (dep[top[x]] < dep[top[top[y]]]) swap(x, y); x = fa[top[x]]; } // 在同一条链,返回深度浅的 return dep[x] < dep[y] ? x : y; } void solve() { int n; cin >> n; for (int i = 2; i <= n; i++) { cin >> fa[i]; g[fa[i]].push_back(i); } DFS1(1, 0); // 第一轮 DFS DFS2(1, 1); // 第二轮 DFS int q; cin >> q; while (q--) { int x, y; cin >> x >> y; cout << LCA(x, y) << '\n'; } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
例-树链剖分
树链剖分
1、树链剖分:输入 $n, m, r, p$ 分别表示树的节点个数、操作个数、根节点序号、模数($n, m \leq 10^5$)。接下来 $n$ 行,输入非负值表示各个节点的初始数值;下面 $n-1$ 行,每行输入 $x, y$ 表示两点间连有一条边。对于 $m$ 个操作,输入 $1\ x\ y\ z$ 表示树上从 $x$ 到 $y$ 的最短路径上所有节点值 $+ z$;输入 $2\ x\ y$ 输出树上从 $x$ 到 $y$ 的最短路径上所有节点值之和;输入 $3\ x\ z$ 表示将以 $x$ 为根的子树内所有节点值 $+ z$;输入 $4\ x$ 输出以 $x$ 为根的子树内所有节点值之和。输出的结果对 $p$ 取模
2、对于区间和维护可以使用线段树,但这是一个树上问题而非连续区间问题,因此可以引入时间戳 $dfn$ 表示 DFS 序,注意重链剖分的 DFS 先走重儿子,这样使得同一重链上的节点 $dfn$ 是连续的,此时便转换成了连续区间,可以根据 $dfn$ 建线段树(如下图,点右侧数字为 $dfn$ 时间戳,线段树处理的区间上红色线段对应图中一条重链)
3、对于题目前两种操作,与求 $lca$ 的思路类似,因为树上两点最短路径为 $x \to lca(x, y) \to y$。实际实现时,是让 $x,y$ 到达 $lca(x,y)$,同样每次将链顶深度较深的点向上跳,但跳跃前要对线段树的区间 $[dfn[top[x]], dfn[x]]$ 进行累加或者求和(处理当前所处链上的需要处理的点,且这段区间一定是连续的);重复操作直至两点在同一重链,则最后一条需要处理的链对应到线段树的区间的下标,为两点中深度较浅的点 $dfn$ 到深度较深的点 $dfn$。例如下图中,处理点 $8$ 到 $7$ 路径上点 $+2$ 的过程为:线段树的区间 $[6,6] + 2$,点 $8$ 跳到 $5$;线段树的区间 $[9, 10] + 2$,点 $7$ 跳到 $1$;线段树的区间 $[1, 3] + 2$,完成操作
4、对于题目后两种操作,对于处理 $x$ 这棵子树,令 $x$ 点的 $dfn[x] = k$,那么这棵子树的所有点的 $dfn$ 范围一定在 $[k, k + sz[x] - 1]$,且该区间一定连续。因此,这两种操作同样是对线段树上这段连续的 $dfn$ 区间进行操作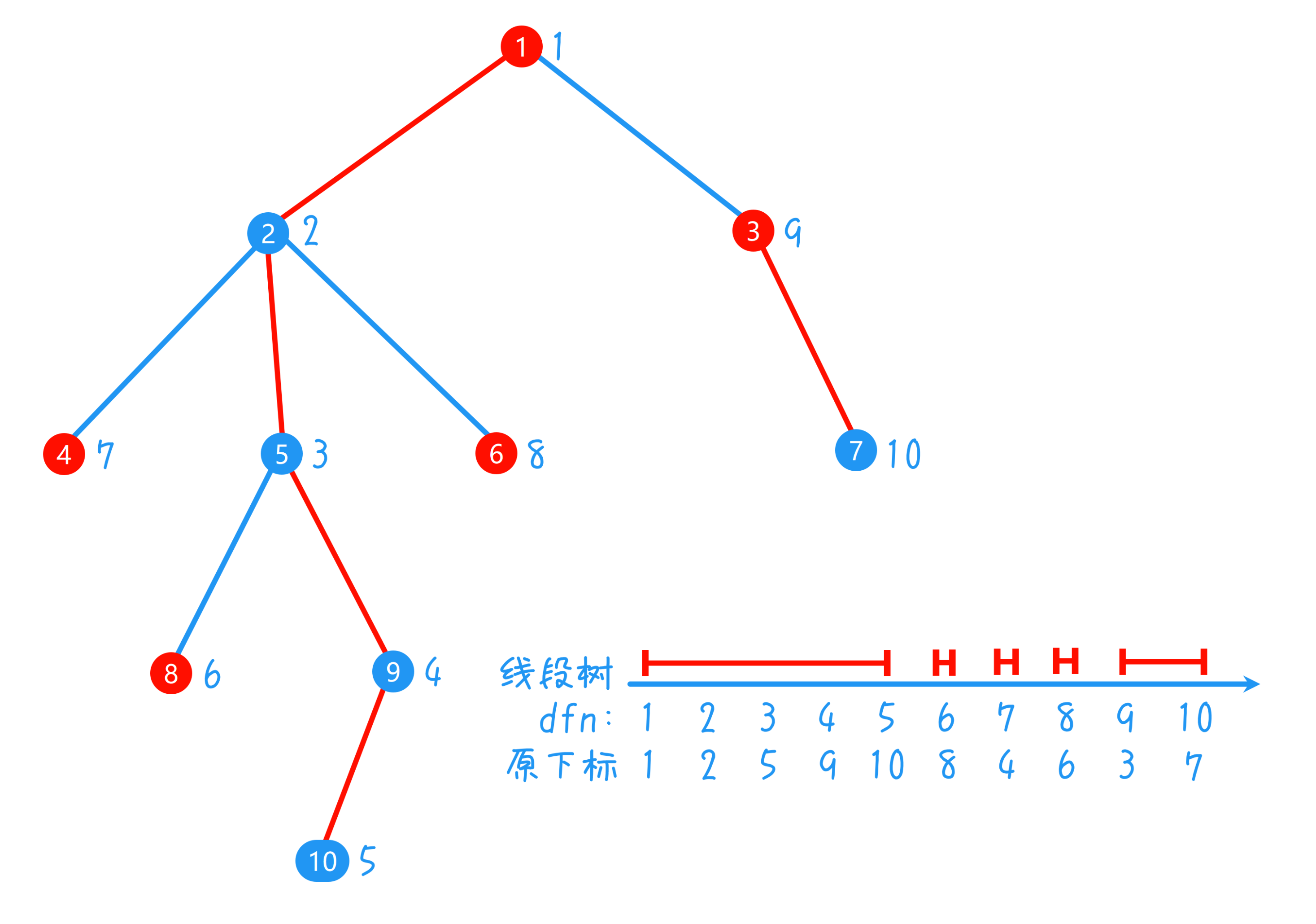
代码实现
#include <bits/stdc++.h> using namespace std; using ll = long long; const int N = 1e5 + 10; ll n, m, r, p; vector<int> g[N]; ll a[N], t[N << 2], lz[N << 2]; // 线段树 ll sz[N], son[N], top[N]; // 重链剖分 ll fa[N], dep[N]; // 父节点和深度 ll dfn[N], idx; // 时间戳 // 求 sz 和 son,建立 fa 和 dep void DFS1(int x, int pre) { sz[x] = 1; fa[x] = pre; dep[x] = dep[pre] + 1; for (auto &y : g[x]) { // 不走父亲 if (y == pre) continue; DFS1(y, x); sz[x] += sz[y]; if (sz[y] > sz[son[x]]) son[x] = y; } } // 求 top,建立 dfn(先走重儿子) void DFS2(int x, int t) { top[x] = t; dfn[x] = ++idx; // 先走重儿子 if (son[x]) DFS2(son[x], t); // 再走轻儿子 for (auto &y : g[x]) { // 额外特判 fa[x],不走父亲 if (y == fa[x] || y == son[x]) continue; DFS2(y, y); } } // 线段树 void pushup(int o) { t[o] = (t[o << 1] + t[o << 1 | 1]) % p; } // buildTree 在 solve() 中直接通过 add() 实现 void update(int s, int e, int o, ll x) { t[o] = t[o] + x * (e - s + 1) % p; lz[o] = lz[o] + x % p; } void pushdown(int s, int e, int o) { if (!lz[o]) return; int mid = (s + e) >> 1; update(s, mid, o << 1, lz[o]); update(mid + 1, e, o << 1 | 1, lz[o]); lz[o] = 0; } void add(int l, int r, ll x, int s = 1, int e = n, int o = 1) { if (l <= s && e <= r) { update(s, e, o, x); return; } pushdown(s, e, o); int mid = (s + e) >> 1; if (mid >= l) add(l, r, x, s, mid, o << 1); if (mid + 1 <= r) add(l, r, x, mid + 1, e, o << 1 | 1); pushup(o); } ll query(int l, int r, int s = 1, int e = n, int o = 1) { if (l <= s && e <= r) return t[o]; pushdown(s, e, o); int mid = (s + e) >> 1; ll res = 0; if (mid >= l) res = (res + query(l, r, s, mid, o << 1)) % p; if (mid + 1 <= r) res = (res + query(l, r, mid + 1, e, o << 1 | 1)) % p; return res; } // 操作 1,将 x y 路径上点 + z void LCA_add(ll x, ll y, ll z) { // 只要不在同一条链上 while (top[x] != top[y]) { // 深度较深的往上跳 if (dep[top[x]] < dep[top[y]]) swap(x, y); // 将要处理的链上的点 + z 再向上跳 add(dfn[top[x]], dfn[x], z); x = fa[top[x]]; } // 在同一条链上,处理剩下的链 if (dep[x] > dep[y]) swap(x, y); add(dfn[x], dfn[y], z); } // 操作 2,求 x y 路径上点之和,由操作 1 修改 ll LCA_sum(ll x, ll y) { ll ans = 0; // 只要不在同一条链上 while (top[x] != top[y]) { // 深度较深的往上跳 if (dep[top[x]] < dep[top[y]]) swap(x, y); // 将要处理的链上的点相加 ans = (ans + query(dfn[top[x]], dfn[x])) % p; x = fa[top[x]]; } // 在同一条链上,处理剩下的链 if (dep[x] > dep[y]) swap(x, y); ans = (ans + query(dfn[x], dfn[y])) % p; return ans; } void solve() { cin >> n >> m >> r >> p; for (int i = 1; i <= n; i++) cin >> a[i]; for (int i = 1; i < n; i++) { int x, y; cin >> x >> y; g[x].push_back(y); g[y].push_back(x); } // 重链剖分 DFS1(r, 0); DFS2(r, r); // buildTree,将 a[i] 按 dfn 对应到线段树上 for (int i = 1; i <= n; i++) add(dfn[i], dfn[i], a[i]); while (m--) { int op; cin >> op; ll x, y, z; if (op == 1) { cin >> x >> y >> z; LCA_add(x, y, z); } else if (op == 2) { cin >> x >> y; cout << LCA_sum(x, y) << '\n'; } else if (op == 3) { cin >> x >> z; // 令 k = dfn[x],将 [k, k + sz[x] - 1] + z add(dfn[x], dfn[x] + sz[x] - 1, z % p); } else { cin >> x; cout << query(dfn[x], dfn[x] + sz[x] - 1) << '\n'; } } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
启发式合并
启发式合并
1、球的颜色:给定 $n, q$ 表示盒子个数和询问次数($n,q \leq 10^5$),给出一个数组 $c[]$,表示初始第 $i$ 个盒子里有一个颜色为 $c_i$ 的球。对于每次询问,输入 $x, y$ 表示将盒子 $x$ 的球全部倒入 $y$ 中,并输出 $y$ 中的球有多少种颜色
2、倒入盒子时球可能有相同的颜色,要处理颜色的种数可以使用set。用set数组维护每个盒子内颜色的状态,放球可以对每个颜色 $i \in x$ 用st[y].insert(i),全部放完后st[x].clear(),每个盒子的颜色种数即为st[y].size()。在此基础上写暴力很简单,但每次合并的操作次数都为 $x$ 的颜色种数,时间复杂度过高
3、先前在并查集中已经接触过启发式合并,其核心思想是让小的指向大的,确保操作次数不超过 $\log$ 次。类比地,该题也可以每次将较小的倒入较大的,按需将 $st[x]$ 和 $st[y]$ 直接交换即可,set的swap操作复杂度是 $O(1)$ 的(底层实现相当于换了指针)
4、对于该题的set的swap是 $O(1)$ 可以直接交换 $st[x]$ 和 $st[y]$,而对于可能的其他数据结构,如果swap复杂度高,可以先只swap(x, y)进行操作,自行标记是否进行了交换,再按需额外用一个map用来映射索引下标,程序使用时使用映射后的下标即可代码实现
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 10; set<int> st[N]; // 维护每个盒子内颜色的情况 void solve() { int n, q; cin >> n >> q; // 初始化盒子 for (int i = 1; i <= n; i++) { int c; cin >> c; st[i].insert(c); } while (q--) { int x, y; cin >> x >> y; // 启发式合并,保证合并时是小的 x 合并到大的 y if (st[x].size() > st[y].size()) swap(st[x], st[y]); for (auto &i : st[x]) st[y].insert(i); st[x].clear(); cout << st[y].size(); } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
例-颜色平衡树
颜色平衡树
1、颜色平衡树:输入 $n$ 表示树的节点数($n \leq 2 \times 10^5$),节点按 $1 \to n$ 编号且 $1$ 为根,对于每个节点,输入 $c, f$ 表示该节点的颜色和父节点编号。如果一棵树中存在的每种颜色的节点数都相同,则称该树为颜色平衡树,输出这棵树中有多少子树是颜色平衡树
2、先想一种暴力的方法:用 $cnt[i]$ 标记颜色 $i$ 当前出现的次数,用一个multiset$st$ 存储所有存在的颜色当前出现次数的状态。addNode()和delNode()函数用于将一个节点的颜色信息向当前状态加入/删除,其更改该点颜色的 $cnt$ 计数,并更新状态 $st$;addTree()和delTree()函数用于将一个子树的颜色信息向当前状态加入/删除,通过 DFS 调用前两个函数实现。主干 DFS 遍历所有节点,每次构建以当前节点为根的子树的状态 $st$,判断 $st$ 中的最大最小值是否相等(即所有颜色计数相同),判断是否是颜色平衡树,判断后再将状态 $st$ 置空。暴力的具体实现如下,显然,构造每棵子树的状态都要跑一次 DFS,复杂度很高,需要优化
3、对于上面暴力的做法,每棵子树状态求完后都直接删除掉了,再求父节点子树的状态时又重新求了一遍,可以想象子节点子树的状态在求父节点子树的状态时是可以复用的。理想情况下,$x$ 的所有子节点 $y$ 的子树的状态加上 $x$ 的信息就是父节点 $x$ 子树的状态,但我们的状态 $st$ 是动态维护的,不能把每个子节点子树的状态离线保留,不过可以在线地保留最后处理的子节点子树的状态,留至递回父节点后处理父节点子树时使用。因此,暴力中的删除操作不再在构建子树状态后直接删除,而是交由父节点控制删除哪些子节点子树的状态,并将最后处理的一棵子节点子树的状态在线地保留,这样当处理父节点子树状态时,可以少处理一颗子树
4、此时,仍需要重复处理的是保留的子树外其他的子节点子树状态,可以看作将这些子树的状态合并到保留子树的状态上,那么便可以使用启发式合并的思路。对于保留的子树,一定含有的信息越多越好,能更有效地减少重复处理,那么便可以重链剖分,保留重儿子子树的状态,让其最后被处理并在线地保留。递回到父节点时,再重复处理轻儿子子树的状态并合并,最后加上父节点信息,便得到父节点子树的状态。由于采用启发式合并,便使得每个点被添加和删除操作至多 $\log$ 次。启发式合并优化后的代码实现如下,主要添加了重链剖分,修改了主干 DFS 的添加和删除的逻辑暴力实现(复杂度过高需要优化)
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; vector<int> g[N]; int ans; int c[N]; // 记录每个节点的颜色 int cnt[N]; // cnt[i] 表示当前颜色 i 的出现次数 multiset<int> st; // st 维护当前所有存在的颜色出现次数的状态 (multiset 允许存储多个相同值且所有值按升序排列) // 将一个节点的颜色信息加入当前状态 void addNode(int x) { // 先将原来 st 中对应颜色的计数信息删除 if (cnt[c[x]]) st.erase(st.find(cnt[c[x]])); // cnt 该点颜色计数 +1,判断该颜色存在(计数不为 0),将计数信息加入状态 st if (++cnt[c[x]]) st.insert(cnt[c[x]]); } // 将一个节点的颜色信息从当前状态删除 void delNode(int x) { // 先将原来 st 中对应颜色的计数信息删除 if (cnt[c[x]]) st.erase(st.find(cnt[c[x]])); // cnt 该点颜色计数 -1,判断该颜色存在(计数不为 0),将计数信息加入状态 st if (--cnt[c[x]]) st.insert(cnt[c[x]]); } // 将以 x 为根的整棵子树的颜色信息加入当前状态 void addTree(int x) { // 加上自己的信息,再 DFS 把所有儿子的信息加上 addNode(x); for (auto &y : g[x]) addTree(y); } // 将以 x 为根的整棵子树的颜色信息从当前状态删除 void delTree(int x) { // 删除自己的信息,再 DFS 把所有儿子的信息删除 delNode(x); for (auto &y : g[x]) delTree(y); } // 主干 DFS void DFS(int x) { // 深度优先处理所有子树 for (auto &y : g[x]) DFS(y); // --此时状态为空--,将 x 子树的信息加入状态 addTree(x); // --此时状态中只有 x 子树信息-- // 如果 st 的最小值等于最大值(所有存在的颜色计数都相同),是颜色平衡树 if (*st.begin() == *st.rbegin()) ans++; // 将所有信息清空,状态回到空 delTree(x); } void solve() { int n; cin >> n; for (int i = 1; i <= n; i++) { int fa; cin >> c[i] >> fa; g[fa].push_back(i); } DFS(1); cout << ans; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }启发式合并优化
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; vector<int> g[N]; int ans; int c[N]; // 记录每个节点的颜色 int cnt[N]; // cnt[i] 表示当前颜色 i 的出现次数 multiset<int> st; // st 维护当前所有存在的颜色出现次数的状态 (multiset 允许存储多个相同值且所有值按升序排列) int sz[N], son[N]; // 重链剖分 // 将一个节点的颜色信息加入当前状态 void addNode(int x) { // 先将原来 st 中对应颜色的计数信息删除 if (cnt[c[x]]) st.erase(st.find(cnt[c[x]])); // cnt 该点颜色计数 +1,判断该颜色存在(计数不为 0),将计数信息加入状态 st if (++cnt[c[x]]) st.insert(cnt[c[x]]); } // 将一个节点的颜色信息从当前状态删除 void delNode(int x) { // 先将原来 st 中对应颜色的计数信息删除 if (cnt[c[x]]) st.erase(st.find(cnt[c[x]])); // cnt 该点颜色计数 -1,判断该颜色存在(计数不为 0),将计数信息加入状态 st if (--cnt[c[x]]) st.insert(cnt[c[x]]); } // 将以 x 为根的整棵子树的颜色信息加入当前状态 void addTree(int x) { // 加上自己的信息,再 DFS 把所有儿子的信息加上 addNode(x); for (auto &y : g[x]) addTree(y); } // 将以 x 为根的整棵子树的颜色信息从当前状态删除 void delTree(int x) { // 删除自己的信息,再 DFS 把所有儿子的信息删除 delNode(x); for (auto &y : g[x]) delTree(y); } // 重链剖分处理 size[] 和 son[] void DFS1(int x) { // 先将每个新点自己的大小标记为 1 sz[x] = 1; // 遍历子节点 for (auto &y : g[x]) { DFS1(y); // 递回时,加上子节点子树的大小 sz[x] += sz[y]; // 如果当前子节点 size 最大,标记为 x 的重儿子 if (sz[y] > sz[son[x]]) son[x] = y; } } // 主干 DFS void DFS(int x) { // 父节点控制删除 for (auto &y : g[x]) { // 重儿子先跳过,留到最后处理 if (y == son[x]) continue; // --此时状态为空--,DFS 处理判断轻儿子子树 DFS(y); // --此时状态为 y 子树信息--,删除轻儿子子树 delTree(y); // --此时状态为空-- } // 剩下重儿子没处理,最后处理重儿子(注意判断重儿子是否存在) if (son[x]) DFS(son[x]); // --此时状态为重儿子子树状态--,其状态被在线地保留 // 所有轻儿子子树状态合并到当前状态,再加上 x 自己的节点信息,得到 x 子树信息 for (auto &y : g[x]) { if (y == son[x]) continue; addTree(y); } addNode(x); // --此时状态中只有 x 子树信息-- // 如果 st 的最小值等于最大值(所有存在的颜色计数都相同),是颜色平衡树 if (*st.begin() == *st.rbegin()) ans++; } void solve() { int n; cin >> n; for (int i = 1; i <= n; i++) { int fa; cin >> c[i] >> fa; g[fa].push_back(i); } DFS1(1); DFS(1); cout << ans; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试