树状数组与ST表

---

树状数组

---

• 树状数组

  1、树状数组常用于维护区间和，有以下操作：单点修改 $O(\log n)$，区间修改 $O(\log n)$，区间查询 $O(\log n)$
  2、树状数组的结构如下图，注意树状数组中一定不能用下标 $0$ 。$T[i]$ 所存的值为管辖区间的和，$T[i]$ 所覆盖的管辖区间为 $[i - lowbit(i) + 1, i]$ ，管辖区间长度为 $lowbit(i)$
  3、$lowbit(i)$ 表示 $i$ 的二进制只保留最后一位 $1$ 的结果(例如二进制 $1101100$ 只保留后三位变为 $100$)，公式为 $lowbit(x) = x \land -x$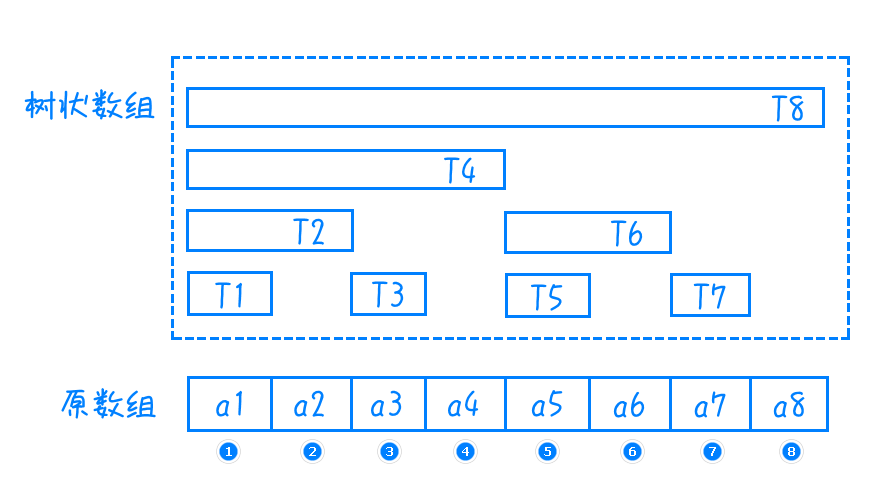

  

• 区间查询

  1、假如需要查询 $[1, 7]$ 的区间和，可以通过树状数组的值进行拼凑，即 $sum = T[7] + T[6] + T[4]$
  2、由于 $T[i]$ 管辖区间长度为 $lowbit(i)$ ，所以很容易就能得到拼凑所需的 $T[i]$ 。如该例首先一定会从 $T[7]$ 开始拼凑，只需要不断迭代 $T[i - lowbit(i)]$ 即可，如 $T[7 - lowbit(7)] = T[6]$、$T[6 - lowbit(6)] = T[4]$、$T[4 - lowbit(4)] = T[0]$ 时结束
  3、注意：这种方法只能得到 $[1, r]$ 的前缀和，如果要求 $[l, r]$ 区间和，需要按照前缀和思路处理 $getsum(r) - getsum(l - 1)$

  const int N = 3e5 + 10;
  int a[N], t[N];   // 原数组与树状数组
  int n;            // 数组大小
  
  int lowbit(int x)
  {
      return x & -x;
  }
  
  // 区间查询
  int getsum(int k)
  {
      int sum = 0;
      for (int i = k; i > 0; i -= lowbit(i))
          sum += t[i];
      return sum;
  }

• 单点修改

  1、假如原数组中 $a[3]$ 的值增加了，在树状数组中覆盖到 $a[3]$ 的 $T[i]$ 都应该增加，即 $T[3]$、$T[4]$、$T[8]$ 应该修改，怎么确定被覆盖的位置？
  2、首先一定会从 $T[3]$ 开始修改，再向后不断迭代 $T[i + lowbit(i)]$ 即可确定其他位置，如 $T[3 + lowbit(3)] = T[4]$、$T[4 + lowbit(4)] = T[8]$ 类推，因此迭代次数是 $\log$ 级

  const int N = 3e5 + 10;
  int a[N], t[N];   // 原数组与树状数组
  int n;            // 数组大小
  
  int lowbit(int x)
  {
      return x & -x;
  }
  
  // 单点修改
  void update(int k, int x)
  {
      for (int i = k; i <= n; i += lowbit(i))
          t[i] += x;
  }

• 区间修改

  1、先前单点修改本质是通过树状数组维护原数组的前缀和，而区间修改则是通过树状数组来维护差分。只需在单点修改基础上做一些修改
  2、区间修改的公式推导如下图，这样便做到了将区间和转换为只需要维护差分即可得到的形式，再令树状数组 $t1[i]$ 维护 $d[i]$ ，$t2[i]$ 维护 $i * d[i]$
  3、注意当前维护的是差分，所以修改时也要按照差分的思想修改。即 $[l, r] + 3$ 需要 $update(l, 3), update(r+1, -3)$

  

  const int N = 3e5 + 10;
  // 树状数组 t1[i] 维护 d[i]，即差分数组 diff，t2[i] 维护 i * d[i]
  int a[N], t1[N], t2[N];
  int n, q;
  
  int lowbit(int x)
  {
      return x & -x;
  }
  
  // 区间修改
  void update(int k, int x)
  {
      for (int i = k; i <= n; i += lowbit(i))
      {
          // 修改维护 t1 和 t2
          t1[i] += x;
          t2[i] += k * x;
      }
  }
  
  // 区间查询
  int getsum(int k)
  {
      int sum = 0;
      for (int i = k; i > 0; i -= lowbit(i))
          sum += (k + 1) * t1[i] - t2[i]; // 推导的公式
      return sum;
  }

---

例-单点修改

---

• 单点修改

  1、单点修改：给定一个长度为 $n$ 的数组 $a$ ，$q$ 次操作。操作有两种：输入 $1, k, v$ 表示 $a[k] += v$ ，输入 $2, l, r$ 表示查询 $[l, r]$ 区间和并输出
  2、对于大多数题目，一开始输入数组 $a$时，应把树状数组每个元素看作值为 $0$，通过单点修改构造初始的树状数组

• 代码实现

  #include <bits/stdc++.h>
  using namespace std;
  
  #define int long long
  const int N = 3e5 + 10;
  int a[N], t[N];   // 原数组与树状数组
  int n, q;         // 数组大小
  
  int lowbit(int x)
  {
      return x & -x;
  }
  
  // 单点修改
  void update(int k, int x)
  {
      for (int i = k; i <= n; i += lowbit(i))
          t[i] += x;
  }
  
  // 区间查询
  int getsum(int k)
  {
      int sum = 0;
      for (int i = k; i > 0; i -= lowbit(i))
          sum += t[i];
      return sum;
  }
  
  void solve()
  {
      cin >> n >> q;
      for (int i = 1; i <= n; i++)
          cin >> a[i];
  
      // 构造树状数组
      for (int i = 1; i <= n; i++)
          update(i, a[i]);
  
      while (q--)
      {
          int op;
          cin >> op;
  
          // 单点修改
          if (op == 1)
          {
              int k, v;
              cin >> k >> v;
              update(k, v);
          }
          // 区间查询
          else
          {
              int l, r;
              cin >> l >> r;
              cout << getsum(r) - getsum(l - 1) << '\n';
          }
      }
  }
  
  signed main()
  {
      ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
      int T = 1;
      // cin >> T;
      while (T--)
          solve();
      return 0;
  }

---

例-区间修改

---

• 区间修改

  1、区间修改：给定一个长度为 $n$ 的数组 $a$，$q$ 次操作。操作有两种：输入 $1, l, r, v$表示原数组区间 $[l, r]$ 累加 $v$，输入 $2, l, r$ 表示查询 $[l, r]$ 区间和并输出
  2、由于维护的是差分，所以修改时要按照差分的思想修改

• 代码实现

  #include <bits/stdc++.h>
  using namespace std;
  
  #define int long long
  const int N = 3e5 + 10;
  // 树状数组 t1[] 维护 d[i]，即差分数组 diff[]，t2[] 维护 i * d[i]
  int a[N], t1[N], t2[N];
  int n, q;
  
  int lowbit(int x)
  {
      return x & -x;
  }
  
  // 区间修改
  void update(int k, int x)
  {
      for (int i = k; i <= n; i += lowbit(i))
      {
          // 修改维护 t1 和 t2
          t1[i] += x;
          t2[i] += k * x;
      }
  }
  
  // 区间查询
  int getsum(int k)
  {
      int sum = 0;
      for (int i = k; i > 0; i -= lowbit(i))
          sum += (k + 1) * t1[i] - t2[i]; // 推导的公式
      return sum;
  }
  
  void solve()
  {
      cin >> n >> q;
      for (int i = 1; i <= n; i++)
          cin >> a[i];
  
      // 构造树状数组
      for (int i = 1; i <= n; i++)
      {
          // 差分思想，对于单点则 d[i] += a[i], d[i+1] -= a[i]
          update(i, a[i]);
          update(i + 1, -a[i]);
      }
  
      while (q--)
      {
          int op;
          cin >> op;
  
          // 区间修改
          if (op == 1)
          {
              int l, r, v;
              cin >> l >> r >> v;
              // 差分思想，d[l] += v, d[r+1] -= v
              update(l, v);
              update(r + 1, -v);
          }
          // 区间查询
          else
          {
              int l, r;
              cin >> l >> r;
              cout << getsum(r) - getsum(l - 1) << '\n';
          }
      }
  }
  
  signed main()
  {
      ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
      int T = 1;
      // cin >> T;
      while (T--)
          solve();
      return 0;
  }

---

例-求逆序对个数

---

• 求逆序对个数

  1、求逆序对个数：给定长度为 $n$ 的数组，求逆序对个数。逆序对为满足 $i \lt j$ 且 $a[i] \gt a[j]$ 的二元组
  2、枚举二元组 $(a, b)$ 的右端点 $b$ ，此时所需树状数组实际可以类比为权值数组(桶)。在向右遍历的过程中，桶中不断加入当前遍历的元素(计数 $+1$)，又由于树状数组的区间和性质，当前桶中所有元素数(通过 $getsum(X.size())$ 得到) 减去 $\leq a[i]$ 的元素数 (通过 $getsum(a[i])$ 得到)，即可得到严格大于 $a[i]$ 的元素数
  3、由于数组中元素少范围大且只需要相对位置信息，可以使用离散化优化程序

• 代码实现

  #include <bits/stdc++.h>
  using namespace std;
  
  const int N = 2e5 + 10;
  int a[N], t[N];
  vector<int> X; // 离散化数组
  
  // 二分查找
  int bs(int key)
  {
      int L = -1, R = X.size();
      int mid;
      while (L + 1 != R)
      {
          mid = (L + R) / 2;
          if (X[mid] < key)
              L = mid;
          else
              R = mid;
      }
      return R + 1; // 树状数组不能维护下标 0，所以 +1
  }
  
  int lowbit(int x)
  {
      return x & -x;
  }
  
  void update(int k, int x)
  {
      for (int i = k; i <= X.size(); i += lowbit(i))
          t[i] += x;
  }
  
  int getsum(int k)
  {
      int res = 0;
      for (int i = k; i > 0; i -= lowbit(i))
          res += t[i];
      return res;
  }
  
  void solve()
  {
      int n;
      cin >> n;
      for (int i = 1; i <= n; i++)
      {
          cin >> a[i];
          X.push_back(a[i]);
      }
  
      // 排序去重
      sort(X.begin(), X.end());
      X.erase(unique(X.begin(), X.end()), X.end());
  
      long long ans = 0;
      for (int i = 1; i <= n; i++)
      {
          // 严格比 a[i] 更大的点的个数，即先前入桶的所有元素个数 - 小于等于 a[i] 的元素个数
          ans += 1LL * getsum(X.size()) - getsum(bs(a[i]));
          // 将 a[i] 的离散化下标 +1，即入桶，标记桶中多了一个 a[i]
          update(bs(a[i]), 1);
      }
      cout << ans;
  }
  
  int main()
  {
      ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
      int T = 1;
      // cin >> T;
      while (T--)
          solve();
      return 0;
  }

---

ST 表

---

• ST 表(稀疏表)

  1、ST 表：输入数列长度 $n$ 和询问次数 $m$ ($n \leq 10^5, m \leq 2 \times 10^6$)，给出数列 $a[]$，对于每个询问，给定 $l\ r$，输出区间 $[l, r]$ 的最大值
  2、ST 表主要用来解决区间最值问题，应用倍增思想，可以做到 $O(n\log n)$ 预处理，$O(1)$ 查询。首先需要预处理：用 $st[i][j]$ 表示以 $i$ 为起点，长度为 $2^j$ 的区间的最大值，如果用两个等长的小区间拼凑一个大区间，有 $st[i][j] = max(st[i][j - 1], st[i + 2^{j-1}][j - 1])$ (分成两个长度为 $2^{j-1}$ 的区间，起点分别为 $i$ 和 $i + 2^{j-1}$)。在实现中，可以直接输入 $a_i$ 到 $st[i][0]$，用 $1 \lt\lt (j-1)$ 表示 $2^{j-1}$；预处理时，第一层循环枚举区间长度 $j$，范围到 $\log_2n$ (通常估取 $20$ 即可)，第二层循环枚举区间起点 $i$，范围满足 $i + 2^j - 1 \leq n$
  3、处理询问时，要对查询区间 $[l, r]$ 进行分割拼凑：先算出询问区间长度 $len = (r-l+1)$ 的指数 $k = \lfloor \log_2 (r-l+1) \rfloor$，列举 $k$ 可能对应的区间长度可知，区间长度满足 $2^k \leq len \lt 2^{k+1}$，即询问区间必然可以用两个长度为 $2^k$ 的区间拼凑得到，起点分别为 $l$ 和 $r - 2^k + 1$
  4、凡是符合结合律且可重复贡献的信息查询都可以使用 ST 表，如最值、最大 gcd/lcm、按位与/或等，如果涉及区间修改，就要使用线段树了

• 代码实现

  #include <bits/stdc++.h>
  using namespace std;
  
  const int N = 1e5 + 10;
  int st[N][1 << 5];
  
  void solve()
  {
      int n, m;
      cin >> n >> m;
  
      // 直接输入 st 表中
      for (int i = 1; i <= n; i++)
          cin >> st[i][0];
  
      // 初始化，j 枚举区间长度，i 枚举区间起点
      for (int j = 1; j <= 20; j++)
          for (int i = 1; i + (1 << j) - 1 <= n; i++)
              st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
  
      // 处理询问
      for (int i = 1; i <= m; i++)
      {
          int l, r;
          cin >> l >> r;
          int k = log2(r - l + 1);                                // 得到区间长度 k
          cout << max(st[l][k], st[r - (1 << k) + 1][k]) << '\n'; // 用长度为 2^k 的区间拼凑
      }
  }
  
  int main()
  {
      ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
      int T = 1;
      // cin >> T;
      while (T--)
          solve();
      return 0;
  }

---

页底评论

---