引入
1、C 与 C++的数据类型表示范围有上限,有时会遇到一些特别大的数据量级,使用
unsigned long long都无法表示
2、此时需要使用高精度算法,当然通常只用来表示数据和做一些简单运算
3、所谓高精度,就是用字符数组来模拟数据运算(运算过程大多模拟竖式运算)
4、下面将介绍一些常用的高精度算法
高精度加法
#include <stdio.h>
#include <string.h>
// 定义两个字符数组,存储高精度数
char s1[1001], s2[1001];
// 定义int类型数组,用来存储转换后的int类型数字
int a[1001], b[1001], c[1001];
int main(void)
{
scanf("%s", s1);
scanf("%s", s2);
// 存储两个高精度数的位数
int la = strlen(s1), lb = strlen(s2);
// 将字符转换为数字,并按照竖式的样式低位对齐存储(倒序转置)
for (int i = 0; i < la; i++)
a[la - i - 1] = s1[i] - '0';
for (int i = 0; i < lb; i++)
b[lb - i - 1] = s2[i] - '0';
/*
此处注意,若
s1 = 12345, s2 = 827
转置后低位对齐:
a = 54321, b = 728
*/
// 相加的结果的位数最大比这两个数中更大的数的位数多1,因为是下标,所以循环时用<=就会直接多1
int lc = la > lb ? la : lb;
// 开始运算,i从lc开始从个位计算,到1为止,因为下标0留给最高位可能的进位
for (int i = 0; i <= lc; i++)
{
// 当前位相加(累加)
c[i] += a[i] + b[i];
// 进位
c[i + 1] = c[i] / 10;
// 处理当前位
c[i] %= 10;
}
// 删除前导0
if (c[lc] == 0 && lc > 0)
lc--;
// 输出,再次翻转倒序
for (int i = lc; i >= 0; i--)
{
printf("%d", c[i]);
}
return 0;
}高精度减法
// 如果 a<b,结果等于 -(b-a),因此应该交换这两个值运算 b-a 再加负号
#include <stdio.h>
#include <string.h>
#include <stdbool.h>
bool flag = false; // 是否需要输出负号
char s1[1001], s2[1001], s3[1001]; // 如果需要交换,则用s3作交换中间值
int a[1001], b[1001], c[1001];
// 比较两个数的大小函数,如果s1 > s2,就返回 true,否则 false
bool compare(char *s1, char *s2)
{
// 先比较位数,位数长的自然大
int u = strlen(s1), v = strlen(s2);
if (u != v)
return u > v;
// 如果位数相同,从前向后(即高位到低位)比较
for (int i = 0; i < u; i++)
if (s1[i] != s2[i])
return s1[i] > s2[i];
// 否则就是完全相同
return true;
}
int main(void)
{
scanf("%s", s1);
scanf("%s", s2);
// 如果 s1 比 s2 大
if (!compare(s1, s2))
{
flag = true;
strcpy(s3, s1);
strcpy(s1, s2);
strcpy(s2, s3);
}
// 这段思路与加法相同,记录位数,转置为int类型
int la = strlen(s1), lb = strlen(s2);
for (int i = 0; i < la; i++)
a[la - i - 1] = s1[i] - '0';
for (int i = 0; i < lb; i++)
b[lb - i - 1] = s2[i] - '0';
// lc 最大即为 la,lb 中的更大者
int lc = la > lb ? la : lb;
// 开始计算
for (int i = 0; i < lc; i++)
{
// 如果需要借位
if (a[i] < b[i])
{
a[i + 1]--;
a[i] += 10;
}
c[i] = a[i] - b[i];
}
// 删除前导0
while (c[lc] == 0 && lc > 0)
lc--;
// 输出
if (flag)
printf("-");
for (int i = lc; i >= 0; i--)
printf("%d", c[i]);
return 0;
}高精度乘法
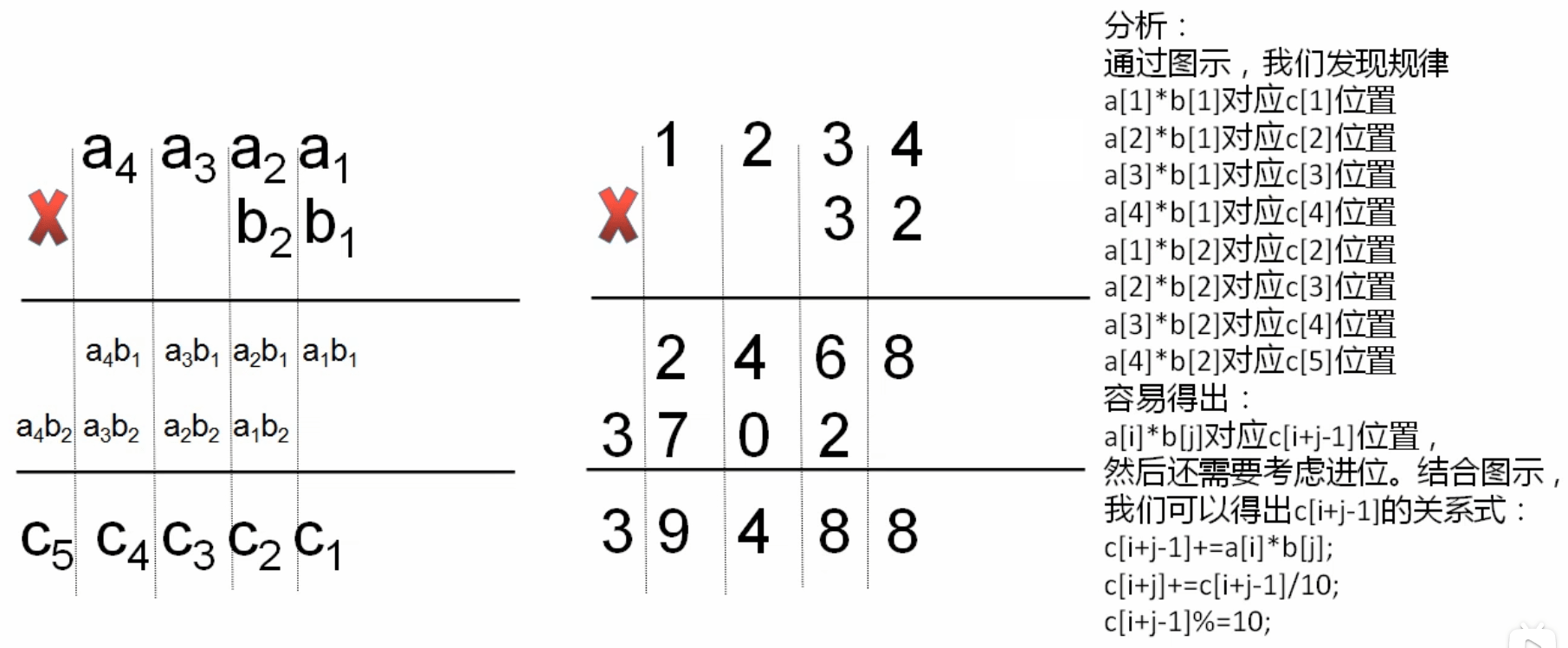
- 注意代码实现与上图不同,代码中的个位下标为 $0$,因此关系式为 $c[i+j] += a[i] * b[j]$
#include <stdio.h>
#include <string.h>
char s1[1001], s2[1001];
int a[1001], b[1001], c[2002]; // c存储乘积,至少应大于a+b的元素之和
int main(void)
{
scanf("%s", s1);
scanf("%s", s2);
int la = strlen(s1), lb = strlen(s2);
for (int i = 0; i < la; i++)
a[la - i - 1] = s1[i] - '0';
for (int i = 0; i < lb; i++)
b[lb - i - 1] = s2[i] - '0';
// c的最高位可能为是a的最高位*b的最高位,因为c的位数最大可能是la + lb
int lc = la + lb;
// 开始计算
for (int i = 0; i < la; i++)
{
for (int j = 0; j < lb; j++)
{
// 计算当前位
c[i + j] += a[i] * b[j];
// 处理进位
c[i + j + 1] += c[i + j] / 10;
c[i + j] %= 10;
}
}
// 删除前导0
while (c[lc] == 0 && lc > 0)
lc--;
// 输出
for (int i = lc; i >= 0; i--)
printf("%d", c[i]);
return 0;
}高精度除法(高/低)
// 思路:按照竖式的思路逐位试商
#include <stdio.h>
#include <string.h>
char s1[1001];
// a为被除数,b为除数,c为商,x用来存储每次试商的余数
long long a[1001], b, c[1001], x = 0;
int main(void)
{
scanf("%s", s1);
scanf("%lld", &b);
int la = strlen(s1);
// 注意被除数不需要转置,因为就是从最高位向低位试商
for (int i = 0; i < la; i++)
a[i] = s1[i] - '0';
for (int i = 0; i < la; i++)
{
c[i] = (x * 10 + a[i]) / b;
x = (x * 10 + a[i]) % b; // 存储余数
}
// 判断商的有效数位,删除前导0
int lc = 0;
while (c[lc] == 0 && lc < la - 1)
lc++;
// 输出
for (int i = lc; i < la; i++)
printf("%d", c[i]);
return 0;
}高精度除法(高/高)
// 思路:使用减法模拟除法
#include <stdio.h>
#include <string.h>
int a[1001], b[1001], c[1001], temp[1001];
// 初始化输入
void init(int x[])
{
char s[1001];
scanf("%s", s);
// 数组的0下标存储位数长度
x[0] = strlen(s);
// 因为需要使用高精度减法实现,所以需要倒序转置
for (int i = 0; i < x[0]; i++)
x[x[0] - i] = s[i] - '0';
}
// 将p数组整体移动n位到q数组中
void numcpy(int p[], int q[], int n)
{
for (int i = 1; i <= p[0]; i++)
q[i + n - 1] = p[i];
q[0] = p[0] + n - 1;
}
// a>b返回1,a=b返回0,a<b返回-1
int compare(int a[], int b[])
{
// 思路与高精度减法的比较函数类似,先比较位数,再按位比较
if (a[0] > b[0])
return 1;
if (a[0] < b[0])
return -1;
for (int i = a[0]; i > 0; i--)
{
if (a[i] > b[i])
return 1;
if (a[i] < b[i])
return -1;
}
return 0;
}
// 高精度减法
void minu(int a[], int b[])
{
for (int i = 1; i <= a[0]; i++)
{
if (a[i] < b[i])
{
a[i + 1]--;
a[i] += 10;
}
a[i] = a[i] - b[i];
}
// 删除前导0,修正位数
while (a[a[0]] == 0 && a[0] > 0)
a[0]--;
}
// 输出函数
void print(int a[])
{
if (a[0] == 0)
{
printf("0");
return;
}
for (int i = a[0]; i > 0; i--)
printf("%d", a[i]);
}
int main(void)
{
// 输入
init(a);
init(b);
// 商的位数最大为 a位数 - b位数 + 1
c[0] = a[0] - b[0] + 1;
// 计算
for (int i = c[0]; i >= 1; i--)
{
memset(temp, 0, sizeof(temp)); // 将temp初始化为0
numcpy(b, temp, i); // 将除数移动i位存入temp
// 模拟减法,如果a>=temp就一直减法
while (compare(a, temp) >= 0)
{
c[i]++;
minu(a, temp);
}
}
// 去除前导0
while (c[c[0]] == 0 && c[0] > 0)
c[0]--;
// 输出
print(c);
printf("\n");
print(a); // a为余数
return 0;
}C++ 高精度加减乘类
#include <iostream>
using namespace std;
struct BigInt
{
BigInt() = default;
BigInt(string s) : len(s.size())
{
for (int i = 0; i < len; i++)
num[len - i - 1] = s[i] - '0';
}
int &operator[](int i)
{
return num[i];
}
void print()
{
if (negative)
cout << '-';
while (num[len] == 0 && len > 0)
len--;
for (int i = len; i >= 0; i--)
cout << num[i];
}
int num[1001] = {}, len = 0;
bool negative = false;
};
BigInt operator+(BigInt &a, BigInt &b)
{
BigInt c;
c.len = max(a.len, b.len);
for (int i = 0; i <= c.len; i++)
{
c[i] += a[i] + b[i];
c[i + 1] = c[i] / 10;
c[i] %= 10;
}
return c;
}
bool compare(BigInt &a, BigInt &b)
{
int len = max(a.len, b.len);
for (int i = len; i >= 0; i--)
{
if (a[i] != b[i])
return a[i] > b[i];
}
return true;
}
BigInt operator-(BigInt &a, BigInt &b)
{
BigInt c, a_, b_;
c.len = max(a.len, b.len);
if (!compare(a, b))
{
c.negative = true;
a_ = b, b_ = a;
}
else
a_ = a, b_ = b;
for (int i = 0; i < c.len; i++)
{
if (a_[i] < b_[i])
{
a_[i + 1]--;
a_[i] += 10;
}
c[i] = a_[i] - b_[i];
}
return c;
}
BigInt operator*(BigInt &a, BigInt &b)
{
BigInt c;
c.len = a.len + b.len;
for (int i = 0; i < a.len; i++)
{
for (int j = 0; j < b.len; j++)
{
c[i + j] += a[i] * b[j];
c[i + j + 1] += c[i + j] / 10;
c[i + j] %= 10;
}
}
return c;
}
int main()
{
string s1, s2;
cin >> s1 >> s2;
BigInt a(s1), b(s2);
BigInt c = a * b;
c.print();
return 0;
}__int128 类型
1、__int128 和 unsigend __int128 这种类型不在 C++ 标准中,所以具体能否使用依赖于编译器是否支持。其表示 128 位 int,且直接支持加减乘除运算
2、int 能表示到约 $10^9$,long long 能表示到约 $10^{18}$,__int128 能表示到约 $10^{38}$
3、但语言自带的输入输出都不能处理这种类型,需要自定义输入输出函数,其基于 C 函数实现,所以不要关闭输入输出同步
4、由于高精度的题即使使用这种类型也不足以表示,自定义函数也过于麻烦,更多的只会用其统计最终答案(可以说只能投机取巧),所以在此只给出输出函数
// __int128 输出函数
void output(__int128 x)
{
if (x >= 10)
output(x / 10);
putchar(x % 10 + '0');
}
// 128 位 int 使用例
__int128 ans = 1;
for (char &i : vec)
ans *= i;
output(ans);


如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试