权值线段树
权值线段树
1、权值线段树:输入操作次数 $q$ ($q \leq 2 \times 10^5$),起始你有一个空的多重集合(允许元素多次出现),对于每次操作:输入 $1\ x$ 表示向集合添加元素 $x$,输入 $2\ l\ r$ 查询大小在 $[l, r]$ 之间的元素个数,输入 $3\ k$ 查询集合中第 $k$ 小的元素
2、先前介绍的线段树用于维护原数组的区间信息,而权值线段树用于维护数组元素的某种属性,例如元素出现次数或其他权值(但一般就是维护元素出现次数,即维护元素出现次数这个桶),数据结构上与线段树类似
3、以维护元素出现次数为例,原数组若为 $\{1, 2, 1, 3, 5\}$ ,则元素出现次数的桶内为 $\{[1]:2,\ [2]:1,\ [3]:1,\ [4]:0,\ [5]:1\}$ 。给这个桶建立线段树即为权值线段树,每个节点的管辖区间表示管辖数字的范围,权值为管辖范围内这些数字的出现次数,如节点 $\{[1, 4] : 4\}$ 表示数字 $1 \to 4$ 共出现了 $4$ 次(下图为线段树结构,请按上述描述类比理解权值线段树的结构),树的叶子结点从左至右对应这个桶本身且管辖区间(对应桶的下标,也即元素值)从左至右都是升序的
4、权值线段树可以进行的操作有单点更新(不依赖 $lazytag$,插入一个元素时更新线段树权值)、数量查询(查询整个数组中元素大小在 $[l, r]$ 之间的元素个数)、数值查询(查询整个数组中第 $k$ 大/小的元素值),所有操作从根节点开始。单点更新,与线段树搜寻策略相同,但可以搜寻过程中直接更新权值(因为不需要维护 $lazytag$),当然也可以找到叶子后递回时pushup。数量查询,即对桶求区间和,在权值线段树上的处理和加法线段树是相同的,凑出完整的询问区间求和即可
5、数值查询,查找第 $k$ 小的元素值,从根节点起,看左子节点权值 $t[l]$:由于管辖区间(对应桶的下标,也即元素值)从左至右都是升序的,权值 $t[l]$ 则表示前 $t[l]$ 小的元素都在左子节点区间。如果 $t[l] \geq k$,说明第 $k$ 小在左子节点区间,应向左继续查找第 $k$ 小;否则,则应向右查找第 $k - t[l]$ 小的元素(因为左区间有 $t[l]$ 个更小的元素,向右查询时应减去 $t[i]$ 排除掉这些元素);最后,应查找到一个叶子结点,其管辖区间即为所求元素值。类似地,查找第 $k$ 大时应判断右子节点权值,如果 $t[r] \geq k$ 则向右查第 $k$ 大,否则向左查第 $k - t[r]$ 大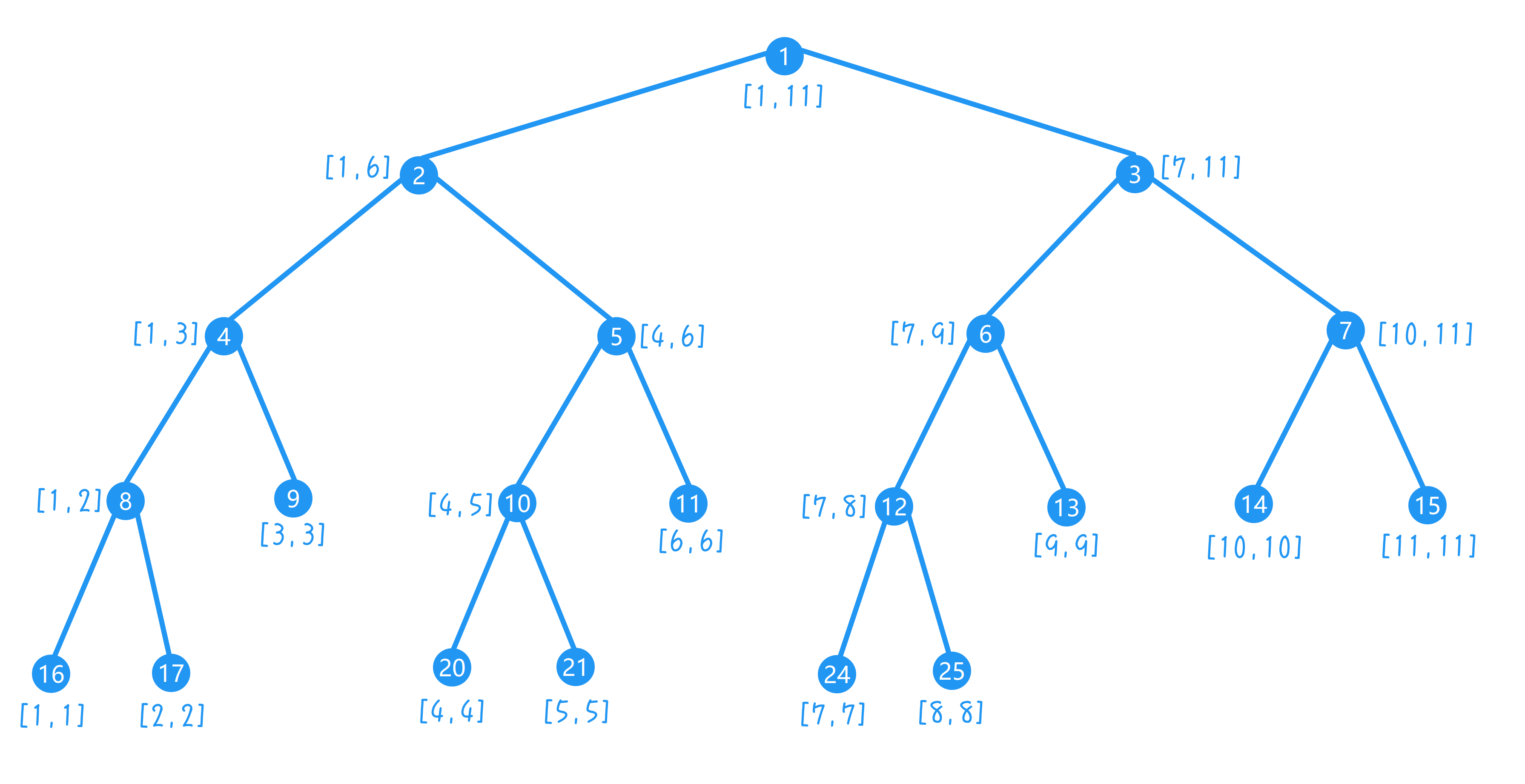
代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; int n = 2e5; // 预想足够的元素个数 int t[N << 2]; // 权值线段树 // 上拉操作 void pushup(int o) { t[o] = t[o << 1] + t[o << 1 | 1]; } // 插入元素 void insert(int x, int s = 1, int e = n, int o = 1) { // 到达叶子结点,计数 +1 if (s == e) { t[o]++; return; } int mid = (s + e) >> 1; // 向左走 if (x <= mid) insert(x, s, mid, o << 1); // 向右走 else insert(x, mid + 1, e, o << 1 | 1); pushup(o); } // 数量查询,查找大小在 [l, r] 的元素个数 int queryCnt(int l, int r, int s = 1, int e = n, int o = 1) { if (l <= s && e <= r) return t[o]; int res = 0; int mid = (s + e) >> 1; // 判断是否需要向左走,如果左子区间 [s, mid] 与 [l, r] 有交集,就要走 if (mid >= l) res += queryCnt(l, r, s, mid, o << 1); // 判断是否需要向右走,如果右子区间 [mid + 1, e] 与 [l, r] 有交集,就要走 if (mid + 1 <= r) res += queryCnt(l, r, mid + 1, e, o << 1 | 1); return res; } // 数值查询,查找第 k 小的元素 int queryVal(int k, int s = 1, int e = n, int o = 1) { // 到达叶子结点,返回管辖区间(所求元素) if (s == e) return s; int mid = (s + e) >> 1; // 看左子节点的权值 int leftsum = t[o << 1]; // 向左走 if (leftsum >= k) return queryVal(k, s, mid, o << 1); // 向右走 else return queryVal(k - leftsum, mid + 1, e, o << 1 | 1); } void solve() { int q; cin >> q; while (q--) { int op; cin >> op; if (op == 1) { int x; cin >> x; insert(x); } else if (op == 2) { int l, r; cin >> l >> r; cout << queryCnt(l, r) << '\n'; } else { int k; cin >> k; cout << queryVal(k) << '\n'; } } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
主席树
主席树(可持久化权值线段树)
1、主席树:给定数组长度 $n$ 和询问次数 $q$ ($n,q \leq 2 \times 10^5$),给出数组 $a[]$。对于每一次询问,给出 $l, r, k$,输出在区间 $[l, r]$ 之间第 $k$ 小的元素
2、上面普通的权值线段树只能在整个数组的范围中进行数量查询和数值查询,如果想要在给定区间内查询,需要用主席树(可持久化权值线段树)。主席树不能像传统线段树那样进行自然编号(即就算左边有未使用到的节点,也预留出位置和编号,此时编号 $o$ 的左右子节点编号固定为 $2o$ 和 $2o + 1$),主席树的编号是动态开点的(节点按添加顺序编号,不预留未使用到的位置和编号,因此左右子节点编号不满足固定规则),所以需要建立结构用 $ls, rs$ 分别存储左右子节点的编号。主席树的数组大小通常是 $N \lt\lt 5$ (后面解释),且通常需要配合离散化。此外,用 $idx$ 标记内存池使用的位置(已使用到的编号),那么下次新建节点的编号即为++idx
3、在主席树之前,我们设想一种不现实但可行的方式:由于要维护任意一个区间的权值状态,原先维护的是一个元素出现次数的桶,假设原数组是 $\{1, 2, 1, 3, 2\}$ ,如果令 $C_i$ 表示到第 $i$ 个元素为止的桶的状态,那么有(为方便,在此使桶内第一个数字表示下标 $1$ 而不是 $0$):$C_0 = \{0, 0, 0\}$ ,$C_1 = \{1, 0, 0\}$ ,$C_2 = \{1, 1, 0\}$ ,$C_3 = \{2, 1, 0\}$ ,$C_4 = \{2, 1, 1\}$ ,$C_5 = \{2, 2, 1\}$ 。可以发现,桶的状态是满足前缀和关系的,如果要求区间 $[2, 4]$ 的桶的状态,可以 $C_4 - C_1 = \{1, 1, 1\}$ ,因此 $n$ 个桶便得到了任意区间的桶的状态。又因为,先前权值线段树就是维护这些桶的信息的,所以给这 $n$ 个桶分别建立自己的权值线段树,便有了 $n$ 棵权值线段树 $t_0, t_1, t_2, \ldots, t_n$ (如下图)。类似地,如果得到区间 $[l, r]$ 的权值线段树,那么对于每个节点 $o$ 通过 $t_r[o] - t_{l-1}[o]$ 计算即可,这样就能得到任意区间的权值线段树
4、观察这几棵权值线段树发现,每次更新节点都只会更新一条路径(图中红色的权值),即只会更新 $\log_2n$ 个节点,其余的点均可复用。那么,我们令 $t_0$ 为起始的树,根为 $rt_0$,那么:对于 $t_1$,先新建根节点 $rt_1$ 并更新,其左子节点需要更新,因此建立新节点并更新左子节点;右子节点不需要更新,因此直接复用 $t_0$ 的对应节点,以此类推,对于 $t_2$ 也同理,这便是主席树的结构。主席树需要的空间为 $n\log_2m$ (其中 $m$ 为元素最大值),但如果最大值过大通常会使用离散化优化,所以通常 $m \leq n$,即看作需要 $n\log_2n$ 的空间,在 $n = 2 \times 10^5$ 时,$log_2n \approx 18$,因此至少需要 $18n$ 的空间
5、主席树的区间数值查询(第 $k$ 小):假设求 $[2, 3]$ 第 $2$ 小,那么需要用到 $rt_3$ 和 $rt_1$ 这两棵树,因为树的结构完全相同,所以查找时,在两棵树同步移动,对应节点的权值相减,得到 $[2, 3]$ 的树(实际不需要做出来,此处为方便表达虚构出来)。那么,对于在这棵虚构的树中查找第 $k$ 小,就完全适用先前权值线段树的方法了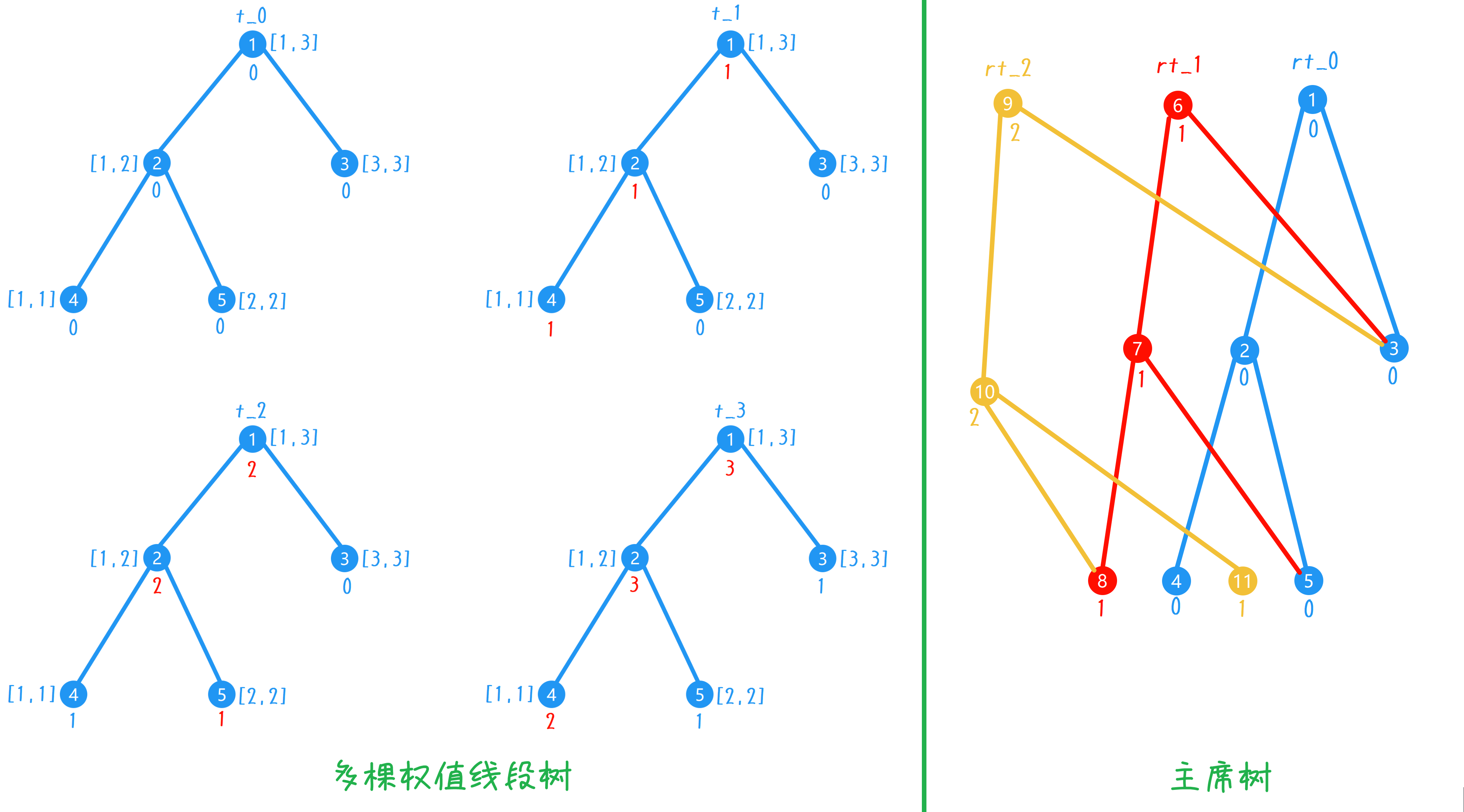
代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; int n, q; int a[N]; // 离散化,bin() 函数用于二分取离散化后的对应值 vector<int> X; int bin(int x) { return lower_bound(X.begin(), X.end(), x) - X.begin() + 1; } // 主席树的结构体 struct Node { int ls, rs; // 左右子节点 int val; // 权值 } t[N << 5]; // 主席树 int rt[N]; // 存储根节点的编号 int idx; // 内存池使用位置 // 动态开点,o 为新开节点(引用类型方便修改),pre 为转移来自的对应节点(上一版本),x 为新加点的权值 void insert(int &o, int pre, int x, int s = 1, int e = n) { o = ++idx; // 分配节点 t[o] = t[pre]; // 复刻上一版本(对应节点),此时节点 t[o] 完全等于 t[pre] t[o].val++; // 修改自身权值(走这条路径,路径上的每个点权值都应该 +1) // 如果已经是叶子结点,结束 if (s == e) return; // 决策下一步 int mid = (s + e) >> 1; // 往左走,左子节点要开点更新。更新 t[o].ls,两棵树同步移动,所以自 t[pre].ls 更新,仍查找 x if (x <= mid) insert(t[o].ls, t[pre].ls, x, s, mid); // 往右走,右子节点要开点更新 else insert(t[o].rs, t[pre].rs, x, mid + 1, e); } // 区间数值查询,lo, ro 是形成区间 [l, o] 权值线段树(虚构的树)所需要的两棵树的对应节点,查找第 k 小 int queryVal(int lo, int ro, int k, int s = 1, int e = n) { // 找到了所求的叶子结点 if (s == e) return s; int mid = (s + e) >> 1; // 看虚构的树的左子节点值 = ro 的左子节点值 - lo 的左子节点值 int leftsum = t[t[ro].ls].val - t[t[lo].ls].val; // 向左走 if (leftsum >= k) return queryVal(t[lo].ls, t[ro].ls, k, s, mid); // 向右走 else return queryVal(t[lo].rs, t[ro].rs, k - leftsum, mid + 1, e); } // 区间数量查询,参数含义同上(该题不需要此函数,仅作为模板演示) int queryCnt(int lo, int ro, int l, int r, int s = 1, int e = n) { if (l <= s && e <= r) return t[ro].val - t[lo].val; int res = 0; int mid = (s + e) >> 1; // 判断是否需要向左走,如果虚构的树左子区间 [s, mid] 与 [l, r] 有交集,就要走 if (mid >= l) res += queryCnt(t[lo].ls, t[ro].ls, l, r, s, mid); // 判断是否需要向右走,如果虚构的树右子区间 [mid + 1, e] 与 [l, r] 有交集,就要走 if (mid + 1 <= r) res += queryCnt(t[lo].rs, t[ro].rs, l, r, mid + 1, e); return res; } void solve() { cin >> n >> q; for (int i = 1; i <= n; i++) cin >> a[i]; // 将数组值离散化 for (int i = 1; i <= n; i++) X.push_back(a[i]); sort(X.begin(), X.end()); X.erase(unique(X.begin(), X.end()), X.end()); // 动态开点建立主席树 for (int i = 1; i <= n; i++) insert(rt[i], rt[i - 1], bin(a[i])); while (q--) { int l, r, k; cin >> l >> r >> k; // X 的下标,queryVal 查到离散化后的下标,由于 vector 从下标 0 记录所以需要 -1 cout << X[queryVal(rt[l - 1], rt[r], k) - 1] << '\n'; } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
主席树-区间不同数的个数
区间不同数的个数
1、区间不同数的个数:给定数组长度 $n$ 和询问次数 $q$ ($n,q \leq 2 \times 10^5$),给出数组 $a[]$。对于每一次询问,给出 $l, r$,输出在区间 $[l, r]$ 之间不同数字的个数
2、以原数组为 $\{1, 2, 1, 2, 2\}$ 为例,另做一个数组 $lst[]$,$lst[i]$ 表示 $a[i]$ 上一次出现的位置(描述数组元素 $a[i]$ 的某种属性),该例为 $\{0, 0, 1, 2, 4\}$ 。求不同数字的个数,可看作求区间内多少数字首次出现,可以发现,区间 $[l, r]$ 内首次出现的数字的 $lst$ 都在所求区间的左范围 $l$ 之前,即 $lst \lt l$,如该例 $[2, 5]$ 之间原数组有 $2, 1$ 首次出现,其对应的 $lst$ 分别为 $0, 1 \lt 2$
3、使用主席树维护 $lst$ 数组(因为其描述数组元素 $a[i]$ 的某种属性),又因为主席树可以进行区间数量查询(得到指定区间内值在 $[l, r]$ 之间的元素个数),那么该题即求指定区间内值在 $[0, l)$ 的元素个数,即为答案代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; int a[N], lst[N]; // lst[i] 记录 a[i] 上一次出现的位置 int n, q; // 离散化 vector<int> X; int bin(int x) { return lower_bound(X.begin(), X.end(), x) - X.begin() + 1; } // 主席树 struct Node { int ls, rs; int val; } t[N << 5]; int rt[N]; // 记录根节点 int idx; // 动态开点,注意 s 从 0 开始,因为 lst 中有值为 0 void insert(int &o, int pre, int x, int s = 0, int e = n) { // 开点,更新 o = ++idx; t[o] = t[pre]; t[o].val++; // 叶子节点退出 if (s == e) return; // 决策左右 int mid = (s + e) >> 1; if (x <= mid) insert(t[o].ls, t[pre].ls, x, s, mid); else insert(t[o].rs, t[pre].rs, x, mid + 1, e); } // 区间数量查询 int queryCnt(int lo, int ro, int l, int r, int s = 0, int e = n) { if (l <= s && e <= r) return t[ro].val - t[lo].val; int res = 0; int mid = (s + e) >> 1; if (mid >= l) res += queryCnt(t[lo].ls, t[ro].ls, l, r, s, mid); if (mid + 1 <= r) res += queryCnt(t[lo].rs, t[ro].rs, l, r, mid + 1, e); return res; } void solve() { cin >> n >> q; for (int i = 1; i <= n; i++) cin >> a[i]; // 离散化 a[] for (int i = 1; i <= n; i++) X.push_back(a[i]); sort(X.begin(), X.end()); X.erase(unique(X.begin(), X.end()), X.end()); // 构造主席树,顺便建立 lst for (int i = 1; i <= n; i++) { insert(rt[i], rt[i - 1], lst[bin(a[i])]); lst[bin(a[i])] = i; } while (q--) { int l, r; cin >> l >> r; cout << queryCnt(rt[l - 1], rt[r], 0, l - 1) << '\n'; // 查询范围 [0, l) } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试