本文程序模板为使用数组下标 0 的模板,如果不使用下标 0,程序可以有所简化,请按照思路自行简化
一维前缀和
例题引入
1、设计一个程序,假如有一个已知长度和数据的数列(如 $\{1, 3, 7, 5, 2\}$ ),程序将 $m$ 次询问该数列的任意区间的区间和 $sum[p, q]$ (例如三次分别询问 $sum[2, 4]$、$sum[0, 3]$、$sum[3, 4]$)
2、简单分析,我们可知如果每次都用循环直接累加,那么单次的时间复杂度为 $O(n)$ ;又因为需要$m$ 次询问,则程序的时间复杂度至少为 $O(n*m)$。显然当数据量较大时,程序的运行速度很慢。而前缀和的时间复杂度只需要 $O(n)$
3、对于这类问题,我们可以通过前缀和来简化程序,具体如下
前缀和数组
1、定义数组 $sum$,其满足:$i=0$ 时, $sum[0] = arr[0]$ ;$i>0$ 时,$sum[i] = sum[i-1] + arr[i]$。该前缀和数组中元素 $sum[i]$ 表示 $[0, i]$ 的区间和
2、如上示例的数列 $\{1, 3, 7, 5, 2\}$,其前缀和数组 $sum$ 的元素为 $\{1, 4, 11, 16, 18\}$。此时,求区间和 $sum[2, 4]$ 便可以简化为 $sum[4] - sum[1]$ ,表示 $sum[0, 4]$ 减去 $sum[0, 1]$
3、因此,我们推导出:$L \gt 0$ 时,$sum[L, R] = sum[R] - sum[L - 1]$ ;$L=0$ 时,$sum[L, R] = sum[R]$
4、更简单的做法是从下标 $1$ 开始使用,可以避免 $i=0$ 的特判(此处未体现)arr 1 3 7 5 2 sum 1 4 11 16 18 代码实现
#include <iostream> using namespace std; const int n = 5; int sum[n]; int get_sum(int L, int R) { if (L != 0) return sum[R] - sum[L - 1]; else return sum[R]; } int main() { int arr[n] = {1, 3, 7, 5, 2}; // 构建前缀和数组 sum[0] = arr[0]; for (int i = 1; i < n; i++) sum[i] = sum[i - 1] + arr[i]; // 计算区间和 cout << get_sum(2, 4) << endl; cout << get_sum(0, 3) << endl; cout << get_sum(3, 4) << endl; return 0; }
一维差分
例题引入
1、设计一个程序,假如有一个已知长度和数据的数列(如 $\{1, 3, 7, 5, 2\}$),程序将给出 $m$ 个操作,每次操作将一个区间 $[p, q]$ 的每个元素加/减给定数值 $v$(例如三次操作分别为 $[2, 4] + 5$、$[1, 3] + 2$、$[0, 2] - 3$),最后所有操作执行后,打印数组数据
2、简单分析,我们可知如果直接对每个元素运算,那么每次操作的时间复杂度为 $O(n)$,则程序的时间复杂度至少为 $O(n*m)$。显然当数据量较大时,程序的运行速度很慢。而差分的时间复杂度只需要 $O(m+n)$
3、对于这类问题,我们可以通过差分来简化程序,具体如下差分数组
1、定义数组 $diff$,其满足:$i=0$ 时,$diff[0] = arr[0]$ ;$i \gt 0$ 时,$diff[i] = arr[i-1] - arr[i]$ 。对差分数组的元素分别求前缀和 $sum\_diff$,便会发现 $sum\_diff = arr$ ,便将差分数组还原回了原数据。差分是前缀和的逆运算
2、如上示例的数列 $\{1, 3, 7, 5, 2\}$,其差分数组 $diff$ 的元素为 $\{1, 2, 4, -2, -3\}$ 。差分标记的具体含义为:对于操作 $[L, R] + v$ ,等价于 $diff[L] + v, diff[R + 1] - v$ 。在差分数组中,在差分标记位加上一个数,相当于标记位以及后面的数都累加该数,在 $R+1$ 的位置再减去这个数,来还原该位以及之后的累加
3、注意:差分只能计算加减,不能计算乘除。此外由于 $diff[R + 1]$ 下标可能超出范围,因此差分数组最好留出富余空间,尽管实际上不操作也不影响答案。差分只适用于多次操作、少次询问的情况(比如该例只在最后询问一次输出),如果需要经常询问需要使用更高级的数据结构(线段树)来解决arr 1 3 7 5 2 diff 1 2 4 -2 -3 sum_diff 1 3 7 5 2 代码实现
1、注意:在代码实现中,通常我们不计算差分数组的值,而只用来记录数值的变化,最后再将原数据 $arr$ 与差分变化的前缀和相加,即 $arr_[i] = arr[i] + sum\_diff[i]$ ,得到最终结果
2、因此程序中 $diff$ 数组通常被初始化为 $0$,用于记录各元素的变化情况。如执行操作 $[1, 2] + 2$ 后,实际数据如下表
3、程序中只需要设计加法函数即可,使用减法时将函数形参取相反数arr 1 3 7 5 2 diff 0 2 0 -2 0 sum_diff 0 2 2 0 0 arr_ 1 5 9 5 2 #include <cstring> #include <iostream> using namespace std; const int n = 5; int diff[n + 1] = {0}; // 表示差分变化的数组,加大一位用来预防处理时越界 // 执行加法 void add(int L, int R, int value) { diff[L] += value; diff[R + 1] -= value; } int main() { int arr[n] = {1, 3, 7, 5, 2}; add(2, 4, 5); add(1, 3, 2); add(0, 2, -3); // 减法将加数取相反数 // 为方便,直接在 diff 上做出前缀和 for (int i = 1; i < n; i++) diff[i] += diff[i - 1]; // 还原原数据,并输出 for (int i = 0; i < n; i++) { arr[i] += diff[i]; cout << arr[i] << ' '; } // 如果程序还有其他询问,可使用 memset 将 diff 置为 0,以准备下次使用 memset(diff, 0, sizeof(diff)); // sizeof(arr) 或写做 n * sizeof(int) return 0; }
二维前缀和
例题引入
1、给定一个 $n \times m$ 的矩阵并已知矩阵内容(如 $3 \times 4$ 的矩阵 $\{\{1,5,6,8\},\{9,6,7,3\},\{5,3,2,4\}\}$),求矩阵中给定范围的区间和 $sum[(x1, y1), (x2, y2)]$ (比如求 $sum[(1, 1), (2, 2)]$ 和 $sum[(0, 1), (1, 3)]$)
2、有了先前一维前缀和的思路,我们可知对此可以用二维前缀和来优化程序二维前缀和
1、定义:数组 $sum[i][j]$ 含义为矩阵和 $sum[(0, 0), (i, j)]$
2、计算公式:$sum[(x1, y1), (x2, y2)] = sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1]$ ,推导过程如下图
3、$sum$ 的初始化:当 $i = 0,j = 0$ 时,$sum[0][0] = arr[0][0]$ ;仅 $i = 0$ 时,看作一维前缀和 $sum[0][j] = sum[0][j - 1] + arr[0][j]$ ;仅 $j=0$ 时,看作竖着的一维前缀和 $sum[i][0] = sum[i - 1][0] + arr[i][0]$ 。初始化好边界后,可以构建整个二维前缀和数组
4、$sum$ 的构建:初始化后其余部分通过从计算公式中逆向运算来构建。设所求的 $sum[i][j]$ 为黄色部分(即 $sum[(0, 0), (i, j)]$ ),用橙色部分 $arr[i][j]$ (当前位置数据,是已知条件中一个定值)加上紫色部分 $sum[i][j - 1]$ (先前计算过的前缀和)和灰色部分 $sum[i - 1][j]$ ,再减去重复部分 $sum[i-1][j-1]$
5、注意:实际运算中,如果遇到 $i = 0$ 或 $j = 0$时,直接套公式会数组越界,需要按情况进行特判。更简单的做法是从下标 $1$ 开始使用,可以避免 $i=0$ 的特判(此处未体现)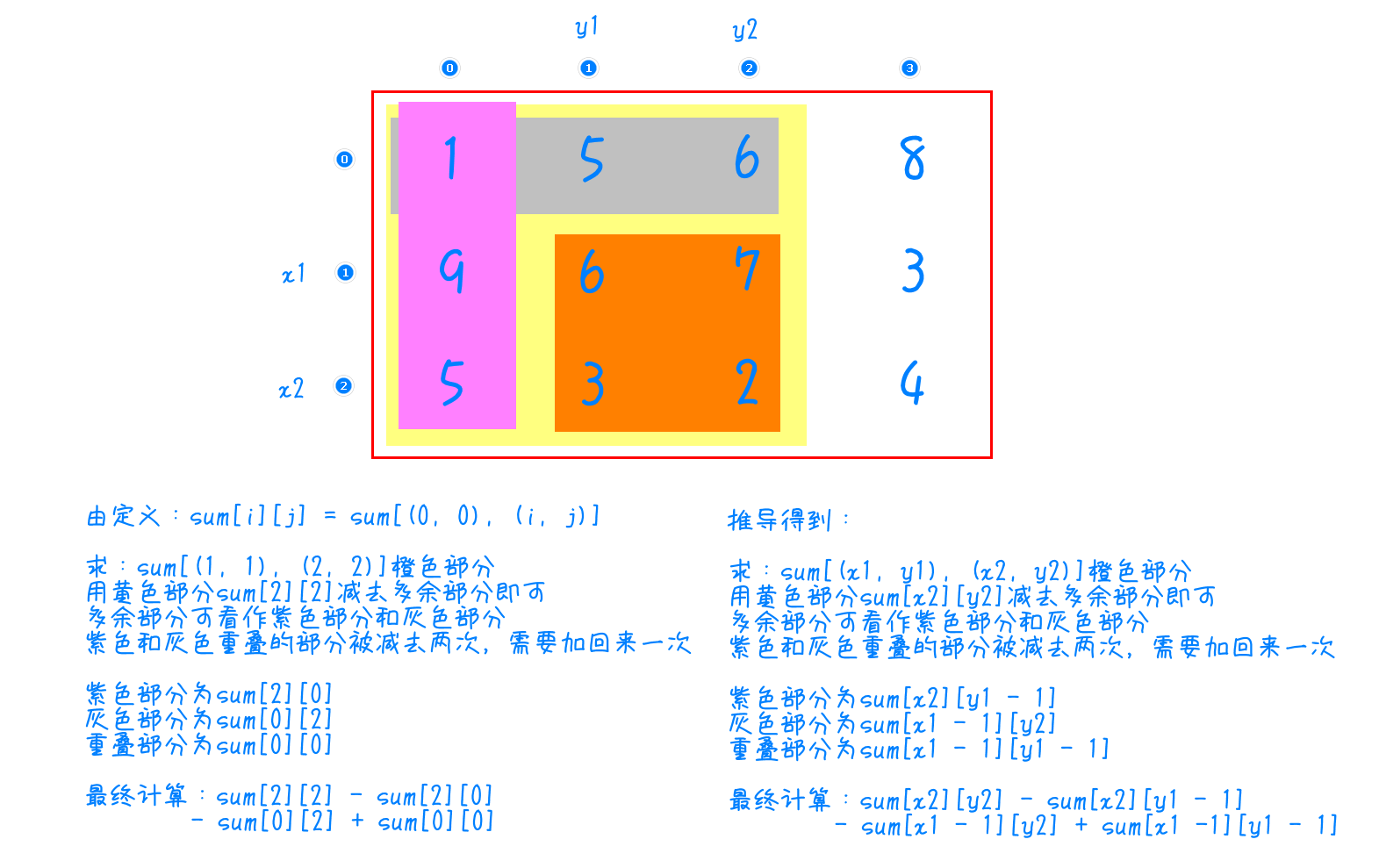
代码实现
#include <iostream> using namespace std; const int n = 3, m = 4; int arr[n][m] = {{1, 5, 6, 8}, {9, 6, 7, 3}, {5, 3, 2, 4}}; int sum[n][m]; // 预处理(初始化 + 构建) void pre_sum() { // i,j 都为0 sum[0][0] = arr[0][0]; // i 为 0,第一行 for (int j = 1; j < m; j++) sum[0][j] = sum[0][j - 1] + arr[0][j]; // j 为 0,第一列 for (int i = 1; i < n; i++) sum[i][0] = sum[i - 1][0] + arr[i][0]; // 构建其他部分 for (int i = 1; i < n; i++) for (int j = 1; j < m; j++) sum[i][j] = arr[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]; } int get_sum(int x1, int y1, int x2, int y2) { // 同 x1 == 0 && y1 == 0,即行和列都是 0,则上方和左边都没有值 if (!x1 && !y1) return sum[x2][y2]; // 同 x1 == 0,即行为 0,则上方没有值,也没有重复部分 if (!x1) return sum[x2][y2] - sum[x2][y1 - 1]; // 列为 0,左边没有值 if (!x2) return sum[x2][y2] - sum[x1 - 1][y2]; // 没有特殊情况,带入完整公式 return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]; } int main() { pre_sum(); cout << get_sum(1, 1, 2, 2) << endl; cout << get_sum(0, 1, 1, 3) << endl; return 0; }
二维差分
例题引入
1、给定一个 $n \times m$ 的矩阵并已知矩阵内容(如 $3 \times 4$ 的矩阵$\{\{1,5,6,8\},\{9,6,7,3\},\{5,3,2,4\}\}$),给出 $m$ 个操作,每次操作将一个区间 $[(x1, y1), (x2, y2)]$ 的每个元素加/减给定数值 $v$(例如两次操作分别为 $[(0, 0), (2, 1)] + 3$ 和 $[(1, 1), (2, 2)] - 1$),最后所有操作执行后,打印数组数据
2、有了先前一维差分的思路,我们可知对此可以用二维差分来优化程序二维差分
1、定义:差分通过标记位来影响标记位之后元素通过前缀和运算还原的数值。因此对数组 $diff[i][j]$ 进行操作,等同于对矩阵 $[(i, j), (n, m)]$ 进行操作(即影响的是标记为到右下角的全部元素)
2、计算公式:$[(x1, y1), (x2, y2)] + v$ 等价于 $diff[x1][y1] += v, diff[x1][y2 + 1] -= v, diff[x2 + 1][y1] -= v, diff[x2 + 1][y2 + 1] += v$ ,推导过程如下图
3、注意:在实际代码设计中,我们通常还是不构造差分数组,只用 $diff$ 记录数值变化,最后再将 $diff$ 前缀和与原数据相加来还原数据。差分数组应该保留富余空间,防止越界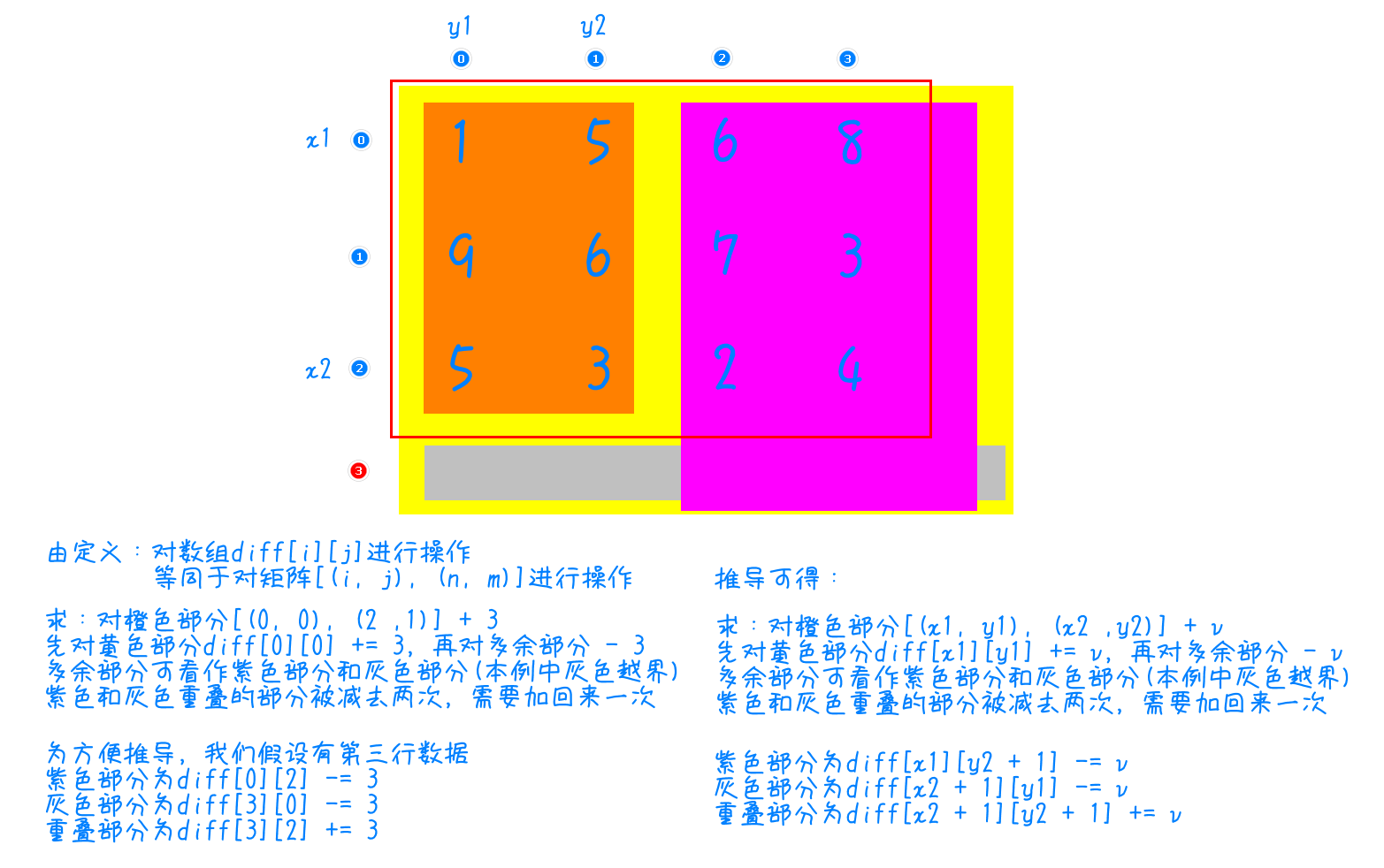
代码实现
#include <cstring> #include <iostream> using namespace std; const int n = 3, m = 4; int arr[n][m] = {{1, 5, 6, 8}, {9, 6, 7, 3}, {5, 3, 2, 4}}; int sum[n][m], diff[n + 1][m + 1]; // diff 开大一些,防止越界 // 差分的处理部分 void add(int x1, int y1, int x2, int y2, int value) { diff[x1][y1] += value; diff[x1][y2 + 1] -= value; diff[x2 + 1][y1] -= value; diff[x2 + 1][y2 + 1] += value; } // 前缀和的处理部分,但对 diff 进行操作,并映射数据回原数组 // 预处理(初始化 + 构建) void pre_sum() { // i,j 都为0 sum[0][0] = diff[0][0]; // i 为 0,第一行 for (int j = 1; j < m; j++) sum[0][j] = sum[0][j - 1] + diff[0][j]; // j 为 0,第一列 for (int i = 1; i < n; i++) sum[i][0] = sum[i - 1][0] + diff[i][0]; // 构建其他部分 for (int i = 1; i < n; i++) for (int j = 1; j < m; j++) sum[i][j] = diff[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]; // 映射数据回原数组 for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) arr[i][j] += sum[i][j]; // 刷新 sum 和 diff 数组以准备下一次运算 memset(sum, 0, sizeof(sum)); memset(diff, 0, sizeof(diff)); } void print() { for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) cout << arr[i][j] << " "; cout << endl; } } int main() { add(0, 0, 2, 1, 3); add(1, 1, 2, 2, -1); pre_sum(); print(); return 0; }
例-鼠鼠我鸭
鼠鼠我鸭
1、鼠鼠我鸭:给定一段序列表示该处为鼠($0$)或鸭($1$),另一段序列给出它们各自的重量,可以进行一次操作或不操作,将一段连续序列中的鼠和鸭转换(鼠变鸭,鸭变鼠,但重量不变),输出可能的鸭子重量之和的最大值
2、先考虑不操作时的鸭子重量之和,将其设为基准值,可通过 $ess += w[i] * a[i]$ 计算(鼠的 $a[i]$ 为 $0$,这样便只计算鸭的重量和了)。进行操作时,如果操作到重 $w[i]$ 的鼠,则实际值应当 $+w[i]$ ,如果操作到重 $w[i]$ 的鸭,则实际值应当 $-w[i]$ 。例如一段动物序列 $\{0, 0, 1, 1, 0\}$ ,其重量为 $\{5, 3, 2, 4, 1\}$ ,那么它们被操作到时,各自产生的偏移量分别为 $\{+5, +3, -2, -4, +1\}$
3、实际值等于基准值+总偏移量,所以要求最大实际值,只需要找到最大的总偏移量。因为操作的序列是连续的,所以可以先做出各自偏移量的前缀和 $prefix$ ,这样总偏移量 $fix$ 就可以通过前缀和的方式 $prefix[i] - prefix[j]$ (其中 $j < i$)得到,即求该式子的最大值。此时可以遍历 $prefix[i]$,只要其左侧的 $prefix[j]$ 是最小值,$fix$ 便是当前最大值
4、其中 $prefix[j]$ 的最小值 $mi$,由于前缀和规定 $j < i$ ,所以可以跟着 $prefix[i]$ 的遍历动态更新,即 $mi = min(mi, prefix[i])$ 。求得当前 $fix$ 最大值后,与先前的 $fix$ 最大值比较,记录最大值 $fix = max(fix, prefix[i] - mi)$ 。最终答案即为 $ess + fix$ (基准值+最大总偏移量)代码实现
#include <bits/stdc++.h> using namespace std; #define int long long const int N = 1e5 + 10; int a[N], w[N], prefix[N]; void solve() { int n; cin >> n; for (int i = 1; i <= n; i++) cin >> a[i]; for (int i = 1; i <= n; i++) cin >> w[i]; // 计算原先不操作时的基准量 int ess = 0; for (int i = 1; i <= n; i++) ess += w[i] * a[i]; // 计算偏移量的前缀和。如果 a[i] 是鼠(0),则偏移量为 +w[i],否则为 -w[i] for (int i = 1; i <= n; i++) prefix[i] = prefix[i - 1] + w[i] * (a[i] ? -1 : 1); // fix 为所求的偏移量,mi 表示 prefix[j] 的最小值,其中 0 <= j < i int mi = 0, fix = 0; for (int i = 1; i <= n; i++) { // 通过前缀和的方式(prefix[i] - prefix[j])计算偏移量,记录偏移量的最大值 fix = max(fix, prefix[i] - mi); // 动态地更新 prefix[j] 的最小值 mi = min(mi, prefix[i]); } cout << ess + fix << '\n'; } signed main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; cin >> T; while (T--) solve(); return 0; }



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试