线段树 | 山暮云秋

加法线段树

线段树

1、先前学习了运用树状数组维护区间和，而线段树是一种更高效更通用的方法，通过 $lazytag$ 优化后可以在 $O(\log n)$ 下完成区间修改和查询(朴素版只能单点修改和区间查询)，还可以维护更多的区间信息(区间和、区间积、异或和、最值等满足可加性或集合合并性质的信息)，运用了分治思想
2、线段树是一种基于二叉树的数据结构，朴素版的每个节点包含的信息有：编号 $o$、管辖区间 $[s, e]$、权值(即维护的区间信息)。为了实现区间修改，还会加入懒标记 $lazytag$
加法线段树

1、加法线段树：给定数组长度 $n$ 和操作次数 $q$ ($n,q \leq 2 \times 10^5$)，再给出数组 $a[]$ 和这 $q$ 次操作。对于每次操作，输入 $1\ l\ r\ x$ 表示将区间 $[l, r]$ 每个元素加上 $x$，输入 $2\ l\ r$ 输出区间 $[l, r]$ 数字之和
2、在线段树中，用一个节点表示一段区间(用管辖区间 $[s, e]$ 记录)。对于编号，运用二叉树的编号性质来构造整棵树，即编号为 $o$ 的节点，左子节点为 $2o = o \lt\lt 1$，右子节点为 $2o + 1 = o \lt\lt 1 \lor 1$，因此，我们需要开 $4n = n \lt\lt 2$ 大小的数组存下这棵树，一般以编号 $1$ 为根。对于管辖区间，先计算节点 $o$ 的中间值 $mid = \lfloor \frac{s + e}{2} \rfloor = (s + e) \gt\gt 1$，则左子节点管辖 $[s, mid]$，右子节点管辖 $[mid + 1, e]$；特别地，如果当前节点区间长度为 $1$，那么没有子节点。线段树结构示意图如下图
3、实现上(可以结合代码理解)，线段树的每次操作都从根开始，因此每个节点的管辖区间都可以由父节点算出来，所以可以不存储管辖区间。上拉操作pushup用子节点的信息更新自己的信息(在此处，当前节点区间和 = 两子节点区间和之和)，该函数也决定线段树的功能。建树buildTree用分治的思想分别建立左右子树，用pushup更新当前节点，建立子树
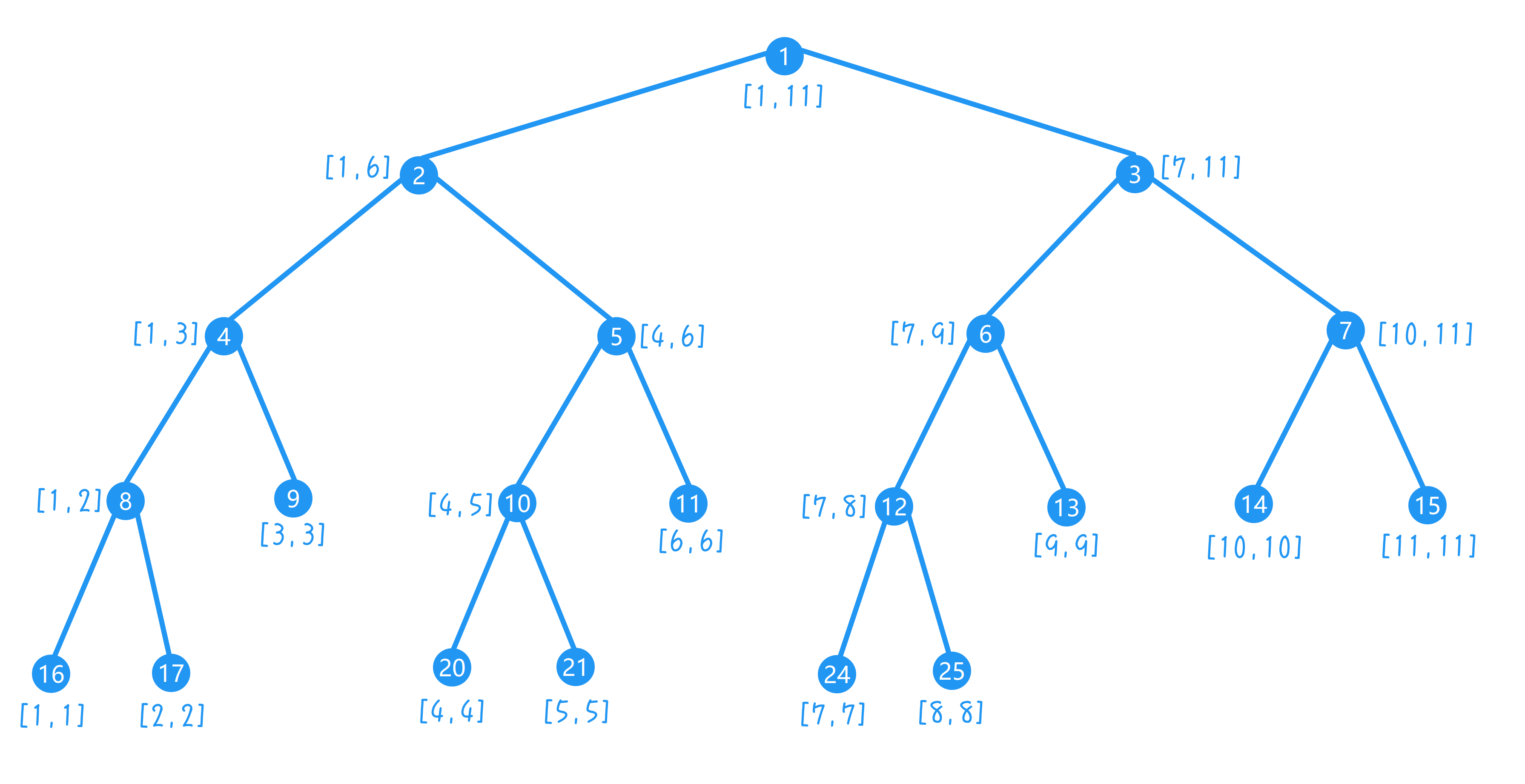
4、线段树的区间修改逻辑(如下图)：例如要修改 $[1, 4] + 2$，从根节点出发，每到一个节点就检查当前管辖区间是否完全包含于目标区间。如果不是，就继续向下找子节点并剪枝(不走与目标节点完全没关系的节点，例如 $[7, 11]$)；如果是，例如 $[1, 3]$，则将该节点权值增加 $2 \times 3 = 6$ (包含 $3$ 个点)，但从此节点开始，向下的整棵子树直至叶子结点都相应地需要更新，全部完成后还要自下而上更新整棵树，对复杂度没有任何优化，为了实现快速的区间修改和查询，必须引入懒标记 $lazytag$
5、$lazytag$ 用于表示某个节点尚未更新给子节点的值(但不是子节点应该加的权值，而是这次任务每元素修改的值)。在上例中，$[1, 3]$ 的节点权值 $+6$，并将其 $lz += 2$，表示该节点自己已更新，但左右子节点都还欠每元素 $+2$ 未更新，该值将在下次经过此节点时下放给子节点。当 $lz = 0$ 表示当前节点左右子节点都已经被更新，相应地，当前节点是否已被更新取决于父节点的 $lz$ 是否为 $0$。注意，使用懒标记必须配合下放操作
6、更新操作update执行更新信息或下放 $lz$ 的具体操作：对于前者，传入待修改值 $x$ 更新该节点权值，并标记 $lz$；对于后者，传入待下放的 $lz$ 更新该节点权值，并继承 $lz$，这两种操作的具体实现是相同的。下放操作pushdown用于每次向下走之前，指挥update向左右子节点下放 $lz$。区间修改add调用整合上述的操作，向下走之前执行下放，查询管辖范围完全在目标区间内的节点，通过update修改它的信息，并在递回时执行上拉更新值。区间查询query与区间修改类似，只做了一点变化
7、此模版使用update作为工具函数，可以提高代码复用性，同时解耦合方便代码功能修改，使得下面其它功能的线段树，只需要稍作修改即可使用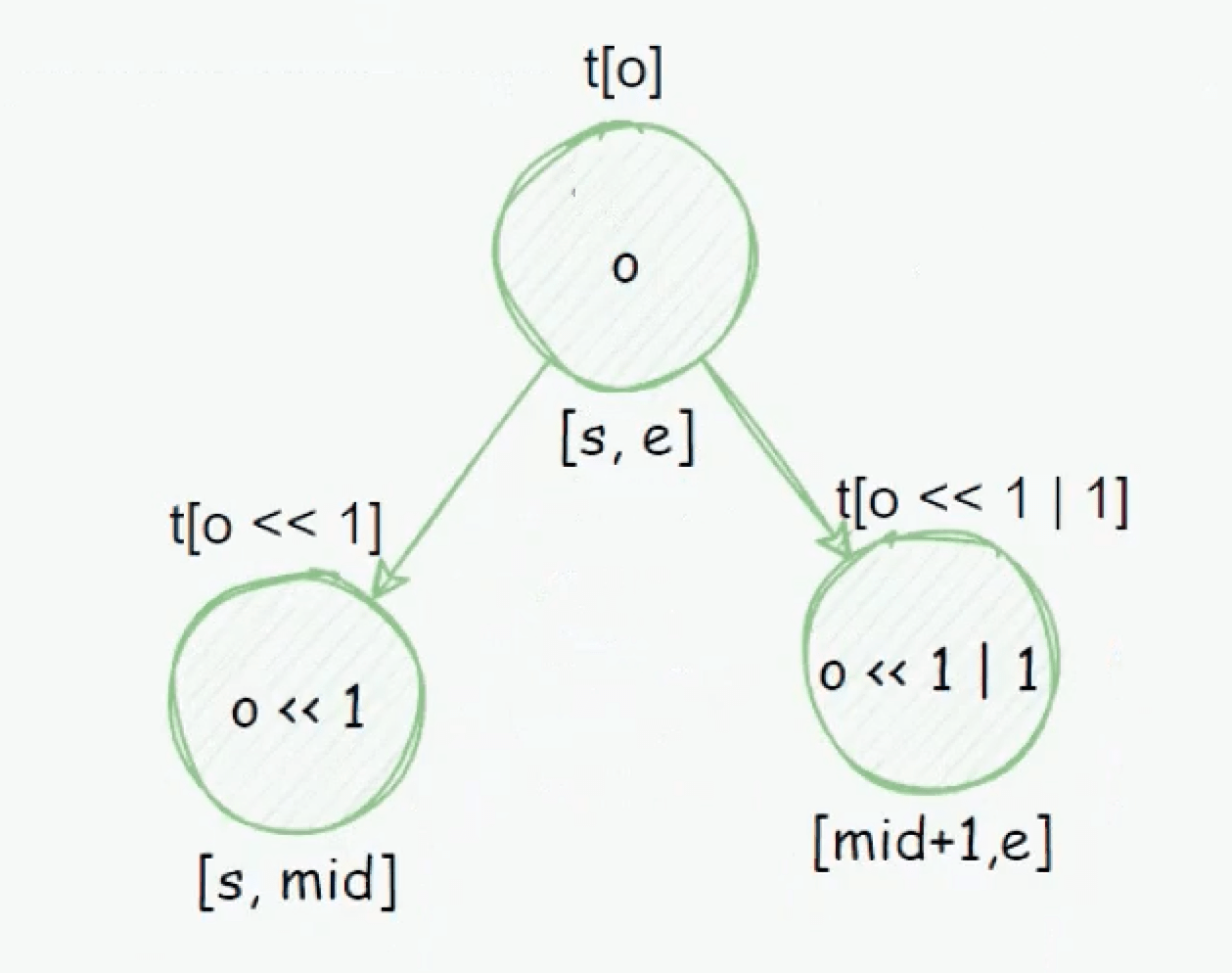

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
using ll = long long;

int n, q;
ll a[N];        // 原数组
ll t[N << 2];   // 线段树，注意大小为 4n = n << 2，t[x] 表示节点 x 所表示的管辖区间(不存储)的元素之和
ll lz[N << 2];  // 懒标记，表示节点 o 尚未更新给子节点的值

// 上拉操作
void pushup(int o)
{
    t[o] = t[o << 1] + t[o << 1 | 1]; // 向上更新父节点
}

// 建树(预设参数)，当前管辖区间 [s, e]，节点编号 o
void buildTree(int s = 1, int e = n, int o = 1)
{
    // 区间长度为 1，得到区间和，结束递归
    if (s == e)
    {
        t[o] = a[s];
        return;
    }

    int mid = (s + e) >> 1;
    buildTree(s, mid, o << 1);         // 左子树
    buildTree(mid + 1, e, o << 1 | 1); // 右子树
    pushup(o);                         // 更新当前节点
}

// 更新操作，当前管辖区间 [s, e]，节点编号 o，需要更新的值 x 或需要下放的 lz
void update(int s, int e, int o, ll x)
{
    // 注意，传入的 x 表示区间里每个点都要 +x，所以要乘上区间长度
    t[o] += x * (e - s + 1); // 更新当前节点的值
    lz[o] += x;              // 标记 lz
}

// 下放操作，当前管辖区间 [s, e]，节点编号 o
void pushdown(int s, int e, int o)
{
    // lz[o] == 0 无需下放
    if (!lz[o])
        return;

    // ls 是左子节点编号，rs 是右子节点编号
    int mid = (s + e) >> 1;
    int ls = o << 1, rs = o << 1 | 1;

    update(s, mid, ls, lz[o]);     // 向左子节点下放 lz
    update(mid + 1, e, rs, lz[o]); // 向右子节点下放 lz

    lz[o] = 0; // 标记下放完成
}

// 区间修改，目标区间 [l, r]，修改值 x，当前管辖区间 [s, e]，节点编号 o
void add(int l, int r, ll x, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
    {
        update(s, e, o, x); // 更新当前节点的值，并标记 lz
        return;             // 不再向下走
    }

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        add(l, r, x, s, mid, o << 1);
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        add(l, r, x, mid + 1, e, o << 1 | 1);

    // 递归回来的时候，记得 pushup
    pushup(o);
}

// 区间查询，目标区间 [l, r]，当前管辖区间 [s, e]，节点编号 o
ll query(int l, int r, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
        return t[o]; // 直接返回当前节点的值

    ll res = 0; // 记录结果

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        res += query(l, r, s, mid, o << 1);
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        res += query(l, r, mid + 1, e, o << 1 | 1);

    // query 没有进行修改，所以可以不 pushup

    return res;
}

void solve()
{
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    buildTree();

    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            ll l, r, x;
            cin >> l >> r >> x;
            add(l, r, x);
        }
        else
        {
            ll l, r;
            cin >> l >> r;
            cout << query(l, r) << '\n';
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

异或线段树

异或线段树

1、异或线段树：给定数组长度 $n$ 和操作次数 $q$ ($n,q \leq 2 \times 10^5$)，再给出数组 $a[]$ 和这 $q$ 次操作。对于每次操作，输入 $1\ l\ r\ x$ 表示将区间 $[l, r]$ 每个元素 $\oplus x$，输入 $2\ l\ r$ 输出区间 $[l, r]$ 数字异或和
2、加法中，pushup是将两个子节点的区间和相加得到当前节点区间和。对于异或，两个子节点的区间异或和相异或得到当前节点区间异或和。因此pushup只需要将 $+$ 改成 $\oplus$ 即可
3、对于update，加法时是加上区间长度个 $x$。对于异或，如果是偶数个数异或相当于不变，如果是奇数个数异或相当于异或一次，因此也修改update。此外，再修改query中统计 $res$ 的部分即可
4、因此，实际只按照异或的规律修改了pushup、update、query

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
using ll = long long;

int n, q;
ll a[N];
ll t[N << 2];
ll lz[N << 2];

// 上拉操作
void pushup(int o)
{
    t[o] = t[o << 1] ^ t[o << 1 | 1]; // 向上更新父节点
}

// 建树(预设参数)，当前管辖区间 [s, e]，节点编号 o
void buildTree(int s = 1, int e = n, int o = 1)
{
    // 区间长度为 1，得到区间和，结束递归
    if (s == e)
    {
        t[o] = a[s];
        return;
    }

    int mid = (s + e) >> 1;
    buildTree(s, mid, o << 1);         // 左子树
    buildTree(mid + 1, e, o << 1 | 1); // 右子树
    pushup(o);                         // 更新当前节点
}

// 更新操作，当前管辖区间 [s, e]，节点编号 o，需要更新的值 x 或需要下放的 lz
void update(int s, int e, int o, ll x)
{
    t[o] ^= ((e - s + 1) & 1 ? x : 0); // 偶数异或 0，奇数异或 x
    lz[o] ^= x;                        // 标记 lz
}

// 下放操作，当前管辖区间 [s, e]，节点编号 o
void pushdown(int s, int e, int o)
{
    // lz[o] == 0 无需下放
    if (!lz[o])
        return;

    // ls 是左子节点编号，rs 是右子节点编号
    int mid = (s + e) >> 1;
    int ls = o << 1, rs = o << 1 | 1;

    update(s, mid, ls, lz[o]);     // 向左子节点下放 lz
    update(mid + 1, e, rs, lz[o]); // 向右子节点下放 lz

    lz[o] = 0; // 标记下放完成
}

// 区间修改，目标区间 [l, r]，修改值 x，当前管辖区间 [s, e]，节点编号 o
void add(int l, int r, ll x, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
    {
        update(s, e, o, x); // 更新当前节点的值，并标记 lz
        return;             // 不再向下走
    }

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        add(l, r, x, s, mid, o << 1);
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        add(l, r, x, mid + 1, e, o << 1 | 1);

    // 递归回来的时候，记得 pushup
    pushup(o);
}

// 区间查询，目标区间 [l, r]，当前管辖区间 [s, e]，节点编号 o
ll query(int l, int r, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
        return t[o]; // 直接返回当前节点的值

    ll res = 0; // 记录结果

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        res ^= query(l, r, s, mid, o << 1);
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        res ^= query(l, r, mid + 1, e, o << 1 | 1);

    // query 没有进行修改，所以可以不 pushup

    return res;
}

void solve()
{
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    buildTree();

    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            ll l, r, x;
            cin >> l >> r >> x;
            add(l, r, x);
        }
        else
        {
            ll l, r;
            cin >> l >> r;
            cout << query(l, r) << '\n';
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

最值线段树

最值线段树

1、最值线段树：给定数组长度 $n$ 和操作次数 $q$ ($n,q \leq 2 \times 10^5$)，再给出数组 $a[]$ 和这 $q$ 次操作。对于每次操作，输入 $1\ l\ r\ x$ 表示将区间 $[l, r]$ 每个元素加上 $x$，输入 $2\ l\ r$ 输出区间 $[l, r]$ 的最大最小值
2、定义 $t_{max}$ 和 $t_{min}$ 两个线段树分别维护最大最小值。类比可知，update中，将区间都加上 $x$，该区间的最大值和最小值都会加上 $x$。pushup中，取两个子节点的 $max$ 或 $min$。buildTree、pushdown、add只需要微修为 $t_{max}$ 和 $t_{min}$。query分为两个函数，一个query_max一个query_min，分别统计即可

代码实现

#include <bits/stdc++.h>
using namespace std;

using ll = long long;
const int N = 2e5 + 10;
const ll INF = 2e18;

int n, q;
ll a[N];
ll t_max[N << 2], t_min[N << 2];
ll lz[N << 2];

// 上拉操作
void pushup(int o)
{
    t_max[o] = max(t_max[o << 1], t_max[o << 1 | 1]);
    t_min[o] = min(t_min[o << 1], t_min[o << 1 | 1]);
}

// 建树(预设参数)，当前管辖区间 [s, e]，节点编号 o
void buildTree(int s = 1, int e = n, int o = 1)
{
    // 区间长度为 1，得到区间和，结束递归
    if (s == e)
    {
        t_max[o] = t_min[o] = a[s];
        return;
    }

    int mid = (s + e) >> 1;
    buildTree(s, mid, o << 1);         // 左子树
    buildTree(mid + 1, e, o << 1 | 1); // 右子树
    pushup(o);                         // 更新当前节点
}

// 更新操作，当前管辖区间 [s, e]，节点编号 o，需要更新的值 x 或需要下放的 lz
void update(int s, int e, int o, ll x)
{
    t_max[o] += x;
    t_min[o] += x;
    lz[o] += x;
}

// 下放操作，当前管辖区间 [s, e]，节点编号 o
void pushdown(int s, int e, int o)
{
    // lz[o] == 0 无需下放
    if (!lz[o])
        return;

    // ls 是左子节点编号，rs 是右子节点编号
    int mid = (s + e) >> 1;
    int ls = o << 1, rs = o << 1 | 1;

    update(s, mid, ls, lz[o]);     // 向左子节点下放 lz
    update(mid + 1, e, rs, lz[o]); // 向右子节点下放 lz

    lz[o] = 0; // 标记下放完成
}

// 区间修改，目标区间 [l, r]，修改值 x，当前管辖区间 [s, e]，节点编号 o
void add(int l, int r, ll x, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
    {
        update(s, e, o, x); // 更新当前节点的值，并标记 lz
        return;             // 不再向下走
    }

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        add(l, r, x, s, mid, o << 1);
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        add(l, r, x, mid + 1, e, o << 1 | 1);

    // 递归回来的时候，记得 pushup
    pushup(o);
}

// 区间查询，目标区间 [l, r]，当前管辖区间 [s, e]，节点编号 o
ll query_max(int l, int r, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
        return t_max[o];

    ll res = -INF; // 记录结果

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        res = max(res, query_max(l, r, s, mid, o << 1));
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        res = max(res, query_max(l, r, mid + 1, e, o << 1 | 1));

    return res;
}

// 区间查询，目标区间 [l, r]，当前管辖区间 [s, e]，节点编号 o
ll query_min(int l, int r, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
        return t_min[o];

    ll res = INF; // 记录结果

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        res = min(res, query_min(l, r, s, mid, o << 1));
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        res = min(res, query_min(l, r, mid + 1, e, o << 1 | 1));

    return res;
}

void solve()
{
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    buildTree();

    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            ll l, r, x;
            cin >> l >> r >> x;
            add(l, r, x);
        }
        else
        {
            ll l, r;
            cin >> l >> r;
            cout << query_max(l, r) << ' ' << query_min(l, r) << '\n';
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

混合线段树

混合线段树

1、混合线段树：给定数组长度 $n$ 和操作次数 $q$ ($n,q \leq 2 \times 10^5$)，再给出数组 $a[]$ 和这 $q$ 次操作。对于每次操作，输入 $1\ l\ r\ x$ 表示将区间 $[l, r]$ 每个元素加上 $x$，输入 $2\ l\ r\ x$ 表示将区间 $[l, r]$ 每个元素乘上 $x$，输入 $3\ l\ r\ x$ 表示将区间 $[l, r]$ 每个元素赋值为 $x$，输入 $4\ l\ r$ 输出区间 $[l, r]$ 数字之和，结果对 $998244353$ 取模
2、由于这道题有三种运算，难以用 $lazytag$ 表示。不妨定义一种运算 $f(val, k, x) = val \times k + x$，那么这三种运算都可以被这种运算表达：赋值 $val \times 0 + x$，乘法 $val \times k + 0$，加法 $val \times 1 + x$。因为这种运算有两个变量，所以需要两个 $lazytag$，分别为乘法标记 $mul[]$ 和加法标记 $add[]$
3、对于核心变化update(s, e, o, k, x)($k, x$ 表示 $val \times k + x$)，设想应该如何更新状态。设区间元素数为 $L$，对于更新权值，乘法在更新时因为有分配律($k \times a_1 + k \times a_2 + k \times a_3 = k \times (a_1 + a_2 + a_3)$)，不需要乘区间元素数，而加法需要。因此得到 $t[o] = t[o] \times k + x \times L$，这样，便得到了权值更新的公式
4、对于更新懒标记，我们令节点 $y$ 的值为 $y$，其父节点为 $o$，那么 $y$ 点的值可以表示为 $t[y] = y = (mul[o]) \times y + (add[o]) \times L$(用权值公式的形式表示，将其记为一式)，现在，假设父节点的 $mul[o], add[o]$ 都已更新，那么对 $y$ 点更新权值，即对一式套用先前推导的权值公式再一次更新 $t[y]$，有 $y’ = (mul[o] \times y + add[o] \times L) \times k + x \times L$，化简得到 $(mul[o] \times k) \times y + (add[o] \times k + x) \times L$(记为二式)，比对一式和二式，即懒标记更新前和更新后的状态，它们都是用 $(A)y + (B)L$ 的形式表示的同构式，分别对比两式的 $A, B$ 部分可以发现，懒标记的更新可以被表示为 $mul[o] = mul[o] \times k$，$add[o] = add[o] \times k + x$
5、$mul[]$ 需要初始化为 $1$，在buildTree中边建树边初始化即可；由于可能有负数，所以写一个取模函数mo处理负数取模；按上述规则完成update，注意取模；pushup、query中需要添加取模；更改pushdown下放 $lazytag$ 的参数和重置的值

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
const int P = 998244353;
using ll = long long;

int n, q;
ll a[N];
ll t[N << 2];
ll add[N << 2], mul[N << 2];

// 取模(处理负数取模)
ll mo(ll x)
{
    return (x % P + P) % P;
}

// 上拉操作
void pushup(int o)
{
    t[o] = mo(t[o << 1] + t[o << 1 | 1]);
}

// 建树(预设参数)，当前管辖区间 [s, e]，节点编号 o
void buildTree(int s = 1, int e = n, int o = 1)
{
    mul[o] = 1; // 初始化

    // 区间长度为 1，得到区间和，结束递归
    if (s == e)
    {
        t[o] = a[s];
        return;
    }

    int mid = (s + e) >> 1;
    buildTree(s, mid, o << 1);         // 左子树
    buildTree(mid + 1, e, o << 1 | 1); // 右子树
    pushup(o);                         // 更新当前节点
}

// 更新操作
void update(int s, int e, int o, ll k, ll x)
{
    // 更新权值，t[o] = t[o] * k + x * Len
    t[o] = mo(mo(t[o] * k) + mo(x * (e - s + 1)));

    // 更新 lazytag，mul[o] = mul[o] * k, add[o] = add[o] * k + x
    mul[o] = mo(mul[o] * k);
    add[o] = mo(mo(add[o] * k) + x);
}

// 下放操作，当前管辖区间 [s, e]，节点编号 o
void pushdown(int s, int e, int o)
{
    // ls 是左子节点编号，rs 是右子节点编号
    int mid = (s + e) >> 1;
    int ls = o << 1, rs = o << 1 | 1;

    update(s, mid, ls, mul[o], add[o]);     // 向左子节点下放 lz
    update(mid + 1, e, rs, mul[o], add[o]); // 向右子节点下放 lz

    mul[o] = 1;
    add[o] = 0;
}

// 区间修改
void modify(int l, int r, ll k, ll x, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
    {
        update(s, e, o, k, x); // 更新当前节点的值，并标记 lz
        return;                // 不再向下走
    }

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        modify(l, r, k, x, s, mid, o << 1);
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        modify(l, r, k, x, mid + 1, e, o << 1 | 1);

    // 递归回来的时候，记得 pushup
    pushup(o);
}

// 区间查询，目标区间 [l, r]，当前管辖区间 [s, e]，节点编号 o
ll query(int l, int r, int s = 1, int e = n, int o = 1)
{
    // 找到管辖区间 [s, e] 完全在目标区间 [l, r] 内的节点
    if (l <= s && e <= r)
        return t[o]; // 直接返回当前节点的值

    ll res = 0; // 记录结果

    // 向下走之前，一定要先下放
    pushdown(s, e, o);

    int mid = (s + e) >> 1;
    // 判断向下走的方向，剪枝
    // 判断是否需要向左走，如果左子区间 [s, mid] 与 [l, r] 有交集，就要走
    if (mid >= l)
        res = mo(res + query(l, r, s, mid, o << 1));
    // 判断是否需要向右走，如果右子区间 [mid + 1, e] 与 [l, r] 有交集，就要走
    if (mid + 1 <= r)
        res = mo(res + query(l, r, mid + 1, e, o << 1 | 1));

    // query 没有进行修改，所以可以不 pushup

    return res;
}

void solve()
{
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    buildTree();

    while (q--)
    {
        int op;
        cin >> op;
        // 加法： * 1 + x
        if (op == 1)
        {
            ll l, r, x;
            cin >> l >> r >> x;
            modify(l, r, 1, x);
        }
        // 乘法： * k + 0
        else if (op == 2)
        {
            ll l, r, k;
            cin >> l >> r >> k;
            modify(l, r, k, 0);
        }
        // 赋值： * 0 + x
        else if (op == 3)
        {
            ll l, r, x;
            cin >> l >> r >> x;
            modify(l, r, 0, x);
        }
        else
        {
            ll l, r;
            cin >> l >> r;
            cout << query(l, r) << '\n';
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

加法线段树

异或线段树

最值线段树

混合线段树

页底评论