倍增 LCA
倍增 LCA
1、LCA:输入树的节点个数 $n$,这棵树以节点 $1$ 为根,接下来 $n-1$ 行,分别输入节点 $2 \to n$ 的父节点,再输入询问次数 $q$,每个询问给出两个整数 $u, v$,输出 $u, v$ 的最近公共祖先 $lca(u,v)$
2、最近公共祖先 LCA:深度最大的公共祖先,即几个节点的父节点链从下向上最早相交的点 (可以是这两个点中的一个)。性质:$u \to v$ 的简单路径可以分为两条链,即 $u \to lca(u,v)$ 和 $lca(u,v) \to v$;类似于 $max, min, gcd$ 等运算,其满足 $lca(x,y,z) = lca(x,lca(y,z))$;多个点的 $lca(x_1,x_2,\ldots,x_k)$ 等价于 DFS 序最小点 和 DFS 序最大点的 $lca$
3、倍增 LCA:类似于 ST 表,我们令 $fa[x][j]$ 表示节点 $x$ 向上走 $2^j$ 所到达的点,例如对于节点 $x$,其向上第一个父节点为 $fa[x][0]$,第二个为 $fa[x][1]$,第四个为 $fa[x][2]$,第八个为 $fa[x][3]$;此外,从根开始以节点深度从上到下标记层次,用 $dep[x]$ 记录 $x$ 的深度。这样的结构可以实现快速跳跃,要从 $x$ 向上跳跃到目标层次,可以贪心地先迈大步再迈小步:从大到小枚举 $j$,再检查 $fa[x][j]$ 是否超过目标层次,超过则不操作,不超过则 $x$ 跳跃到当前 $fa[x][j]$,继续向下枚举。例如,如果要从第 $8$ 层跳跃到第 $2$ 层,二者相隔 $6$ 个节点:为方便,从 $j = 3$ 开始枚举,此时 $fa[x][j]$ 是向上 $8$ 个节点的位置,超出目标范围不操作;继续枚举 $j = 2$,此时 $fa[x][j]$ 为向上 $4$ 个节点的位置,令 $x$ 跳到该位置,此时还差 $2$ 个节点到目标;继续枚举 $j = 1$,$x$ 跳到当前 $fa[x][j]$ 到达目标节点。可以发现,起始相隔的 $6$ 个节点二进制为 $110_2$,$1$ 的位置恰好指示了对应位置 $j$ 需要跳跃
4、实现上,初始化最上面虚拟的点 $fa[1][0] = 0$ (无意义),操作上需要求 $fa[][]$ 数组,再求 $lca$。对于求数组,可以通过 DFS 得到,转移方程为 $fa[x][j] = fa[fa[x][j-1]][j-1]$,例如求 $fa[x][2] = fa[fa[x][1]][1]$ (求 $x$ 向上走 $2^2$ 步,等同于从 $x$ 向上走 $2^1$ 步再走 $2^1$ 步),在 DFS 过程中,上面的点的 $fa[][]$ (即转移方程右侧)是已知的;此外,对于 $dep[]$ 有 $dep[x] = dep[fa[x][0]] + 1$ (深度为父节点 $+1$)。对于求 $lca$,给定两点 $x, y$,首先将深度大的(假设是 $x$)向上跳至二者在同一深度(用上面的方法跳跃),判断 $x, y$ 是否相等(因为可能 $y$ 就是 $x$ 的祖先),相等就输出 $y$;如果不相等,那么二者一起向上跳,依然从大到小枚举 $j$,但条件为若 $fa[x][j] = fa[y][j]$ 则不跳 (始终保持两个点不相等),这样操作后,最终两个点会留在 $lca$ 的子节点,所以返回父节点 $fa[x][0]$ 即为 $lca$代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; int n, q; vector<int> g[N]; // 建图 int fa[N][1 << 5]; // fa[x][j] 记录 x 向上 2^j 的节点编号 int dep[N]; // 记录深度 // DFS 建造 fa[][] 和 dep[] void DFS(int x) { // 求 fa[][] for (int j = 1; j <= 20; j++) fa[x][j] = fa[fa[x][j - 1]][j - 1]; // 深度为父节点 + 1 dep[x] = dep[fa[x][0]] + 1; // 遍历出点,深度优先 for (auto &y : g[x]) DFS(y); } // 求 lca int lca(int x, int y) { // 交换使得 x 深度大 if (dep[x] < dep[y]) swap(x, y); // 深度大的先跳至相同深度 for (int j = 20; j >= 0; j--) // 如果 x 不会跳过头,即 目标点深度 >= y 的深度 if (dep[fa[x][j]] >= dep[y]) // 跳至目标点 x = fa[x][j]; // 判断 x,y 是否相等 if (x == y) return y; // 不相同,两点一起向上跳,至 lca 的子节点 for (int j = 20; j >= 0; j--) // 只要两点目标节点不相同 if (fa[x][j] != fa[y][j]) // 一起向上跳 x = fa[x][j], y = fa[y][j]; // 返回父节点即为 lca return fa[x][0]; } void solve() { cin >> n; for (int i = 2; i <= n; i++) { cin >> fa[i][0]; // 输入 fa[i][0] 父节点 g[fa[i][0]].push_back(i); // 建图 } DFS(1); cin >> q; while (q--) { int x, y; cin >> x >> y; cout << lca(x, y) << '\n'; } } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Tarjan LCA
Tarjan LCA
1、LCA:输入树的节点个数 $n$,这棵树以节点 $1$ 为根,接下来 $n-1$ 行,分别输入节点 $2 \to n$ 的父节点,再输入询问次数 $q$,每个询问给出两个整数 $u, v$,输出 $u, v$ 的最近公共祖先 $lca(u,v)$
2、Tarjan LCA 分为两部分:将询问离线;DFS 过程中用并查集维护 $lca$。初始并查集都指向自己,询问离线后,在 DFS 时对于走过的每个节点,用 $vis$ 标记,再计算深度;第一步先处理子节点,该点所有子节点处理后,递回时第二步看自己有没有询问,第三步将该点的并查集向上合并。该算法实际利用了 DFS 的顺序性质,过程中并查集的根即为下面节点询问的 $lca$
3、具体地,如下图例,其中红色节点为离线后的询问,红虚线表示 DFS 的进度,蓝箭头表示并查集指向:图一,DFS 到节点 $4$ 遇到询问,但没有走到另一个点($vis$ 未被标记)无法处理;图二,从 $4$ 向上过程中更新并查集,到节点 $2$ 发现子节点还未处理完,继续处理子节点,遇到另一个询问 $6$,此时另一个询问 $4$ 已经走过($vis$ 被标记),那么这组询问的答案即为先前询问节点(当前节点并查集还没有指向)的并查集根 $root(4)$;图三,向上返回,并查集向上指向父节点,直至回到 $2$,再向上时 $2$ 才指向 $1$,图例中省略了后面的处理
4、通常倍增 $lca$ 更通用,Tarjan LCA 只能处理离线询问,更常用的还是倍增法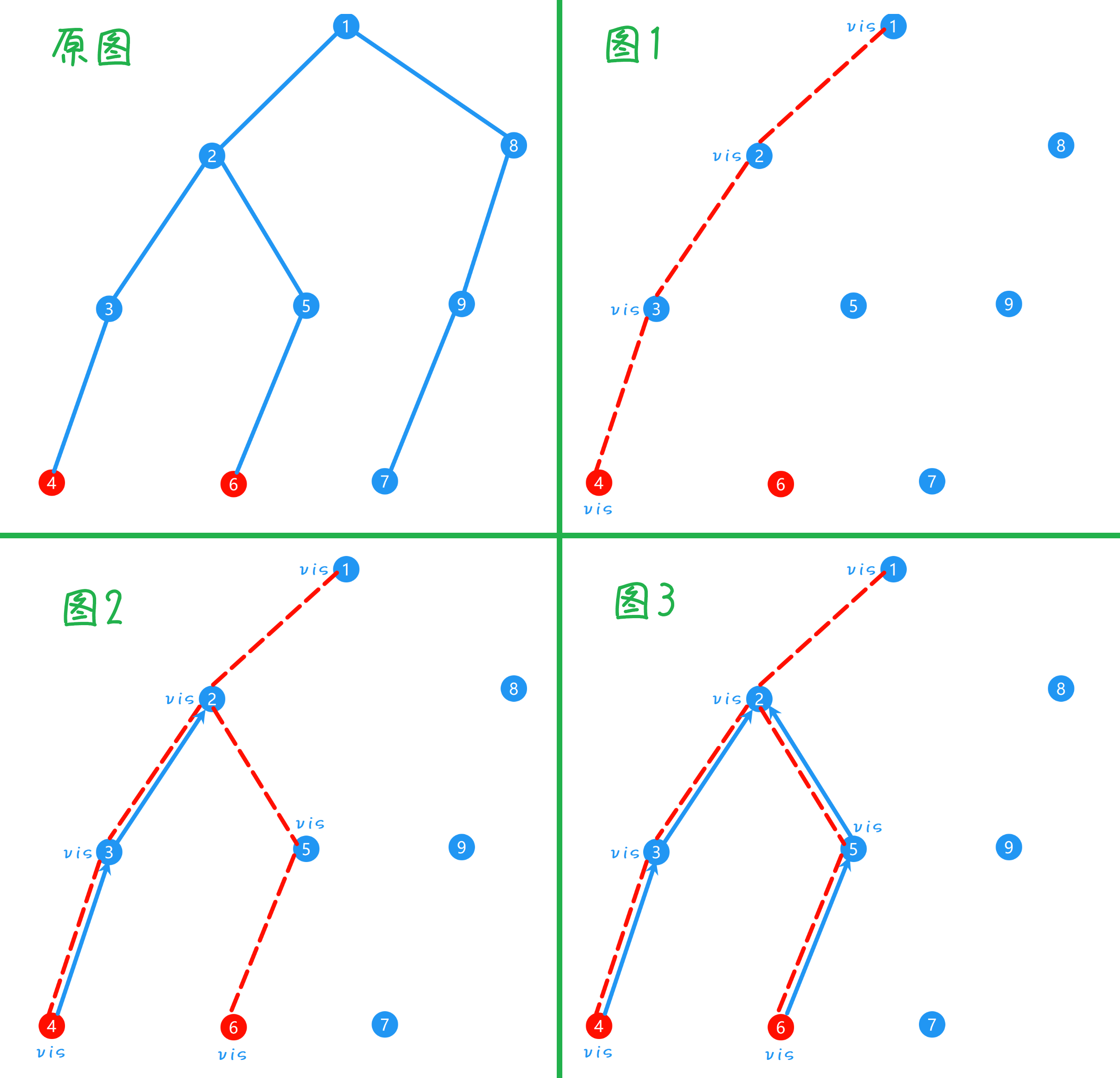
代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; int n, q; vector<int> g[N]; // 建图 bitset<N> vis; // 是否走过 int fa[N]; // 父节点 int dep[N]; // 节点深度 vector<pair<int, int>> Q[N]; // 离线询问,Q[x] 存储有关 x 节点的询问,first 为询问 y,second 为询问编号 int pre[N]; // 并查集 int ans[N]; // 记录答案 // 路径压缩 int root(int x) { return pre[x] = pre[x] == x ? x : root(pre[x]); } // 合并并查集 void merge(int x, int y) { // 将深度大的指向深度小的 int rx = root(x), ry = root(y); if (dep[rx] < dep[ry]) swap(rx, ry); pre[rx] = ry; } // Tarjan LCA,本质是 DFS void Tarjan_LCA(int x) { vis[x] = true; // 标记走过 dep[x] = dep[fa[x]] + 1; // 处理深度 // 处理子节点 for (auto &y : g[x]) Tarjan_LCA(y); // 处理自己的询问 for (auto &[y, id] : Q[x]) { // 如果 y 还未走到,跳过 if (!vis[y]) continue; // 否则该询问的结果为当前并查集的根 ans[id] = root(y); } // 标记,合并并查集 merge(x, fa[x]); } void solve() { cin >> n; for (int i = 2; i <= n; i++) { cin >> fa[i]; g[fa[i]].push_back(i); // 建图 } // 初始化并查集 for (int i = 1; i <= n; i++) pre[i] = i; cin >> q; for (int i = 1; i <= q; i++) { int x, y; cin >> x >> y; // 离线询问,记录询问的编号 i Q[x].push_back({y, i}); Q[y].push_back({x, i}); } Tarjan_LCA(1); for (int i = 1; i <= q; i++) cout << ans[i] << '\n'; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Tarjan 强联通分量
Tarjan 简述
1、Tarjan 指的是一系列算法,包括求强联通分量、割点割边、找环等。本文不讲解 Tarjan 的原理,只介绍具体实现的方式,下面先解释部分名词
2、强联通分量 SCC:图中的一个个任意两点都可以互相到达的最大的连通块(只要是满足条件的最大的连通块都是,并非只能有一个强联通分量),单个点也是一个强联通分量。无向图和有向图中都可以存在:无向图的强联通分量就是子连通块,因为无向图连通的点都可以互相到达,通常不讨论无向图;有向图中需要注意两点能否互相到达,单独的点也是一个强联通分量,如下图中有 $6$ 个强联通分量(红色、黄色、$4$ 个单独的黑色)
3、割点 cut、割边 bridge:仅存在于无向图,有向图没有此概念。一个点若是割点,那么删除该点和与之相连的边后,图不再连通(图中连通块数量 $+1$);一条边若是割边(桥),那么删除该边后,图不再连通。如下图,红色的都是割点,绿色的都是割边
Tarjan 强联通分量
1、有向图缩点:输入点数 $n$ 和边数 $m$ ($n,m \leq 2 \times 10^5$),对于每条边,给出 $x, y$ 表示存在一条 $x$ 到 $y$ 的单向边。输出所有大小 $\gt 1$ 的强联通分量的大小,按从小到大的顺序输出。注意,图不保证连通
2、此处以有向图为例,无向图将其看作有向图实现即可。Tarjan 本质是一个 DFS,所以会构成一棵搜索树,我们通过给节点染色区分强联通分量,颜色相同的点则在同一个强联通分量。对于搜索,用 $dfn[]$ 存储节点的时间戳(被访问的次序),一般认为强联通分量中 $dfn$ 最小的点是根节点(搜索树的根),$dfn[]$ 只初始更新一次,后续是不变的,实际就是 DFS 序,如果 $dfn[x] = 0$ 表示节点 $x$ 从未走过;用 $low[]$ 存储节点能到达的回点(一个走过的点)的最小时间戳(即指向最小的回点),初始时 $low[x] = dfn[x]$ 指向自己,后续始终 $low[x] \leq dfn[x]$ (不可能比自己更大);用 $idx$ 表示此时的时间戳。对于染色,需要栈 $stk[]$ 存储走过且未被染色的点,$col[]$ 存储节点的颜色(可以不用),$scc$ 表示当前的颜色总数(强联通分量总数)
3、算法的流程如下:首先,走到一个新节点 $x$,记录时间戳,更新 $dfn[x]$ 和 $low[x]$,初始时 $low[x] = dfn[x] = ++idx$,将自身入栈。之后,向下看子节点 $y$ 是否是回点:如果是回点($dfn[y] \neq 0$ 且在栈中),不向下走,用回点的 $dfn[y]$ 更新 $low[x] = min(low[x], dfn[y])$;如果不是回点,继续向下走,在后续递回时更新 $low[x] = min(low[x], low[y])$ (此时已经知道该点子节点的 $low[y]$ 了)。当发现某个节点的子节点处理完且 $low[x] = dfn[x]$ 时,即该点是一个根,那么就进行收拢,把下面以它为根的连通块作为一个强联通分量,将栈中元素取出染色,直至自己也完成染色
4、如下图例,为方便理解,虚构一棵搜索树(按 DFS 序建树,不考虑闭回的边,由于 DFS 序可能不同所以树的形式不固定),在图上的 DFS 实际就是对这棵树 DFS,如右图的过程中蓝色箭头所示。图中节点左侧为 $dfn$,右侧为 $low$,蓝色箭头表示 DFS 走过去,红虚箭头表示获取了下一节点但没有走过去,黄虚箭头表示 DFS 递回。图一,按 DFS 到节点 $6$,过程中初始 $dfn, low$ 为时间戳 $idx$,将经过的未染色节点入栈;红虚箭头处,在节点 $6$ 下一个点 $2$ 的 $dfn[2] \neq 0$ (先前走过),更新 $low[6] = min(low[6], dfn[2]) = 2$,表示该点向上最远可以回到 $dfn = 2$ 的点位置。图二,DFS 递回到节点 $3$,更新 $low[3] = min(low[3], low[6]) = 2$,继续递回到节点 $2$,但此时子节点未处理完,继续处理。图三图四的处理同上,最后递回节点 $2$,发现子节点已处理完且 $dfn[2] = low[2] = 2$,该点为根开始收拢,被收拢的点恰是搜索树中 $2$ 的子树所有点,将它们染色记为同一强联通分量,即对栈中节点染色,直至 $2$ 被染色。后续处理同上,在此省略
5、上例是较为简单的情况(只有一棵子树),如果出现另一棵子树指向先前处理过的强联通分量,例如下图原图中 $7$ 指向 $4$,处理 $7$ 时,不能向 $4$ DFS 搜索:从图上看,因为无法从 $4$ 回到 $7$;从实现看,这二者在搜索树上不连通,先前处理完左侧强联通分量后节点出栈,就看作已经完结,搜索树上这棵子树看作被删除,那么搜索树上 $7 \to 4$ 的边不存在。具体地,如先前上面第三条所言,节点向下看之前,要检查节点(在搜索树意义上)是否存在,即检查是否在栈内,实现中用 $ins$ 标记节点是否在栈内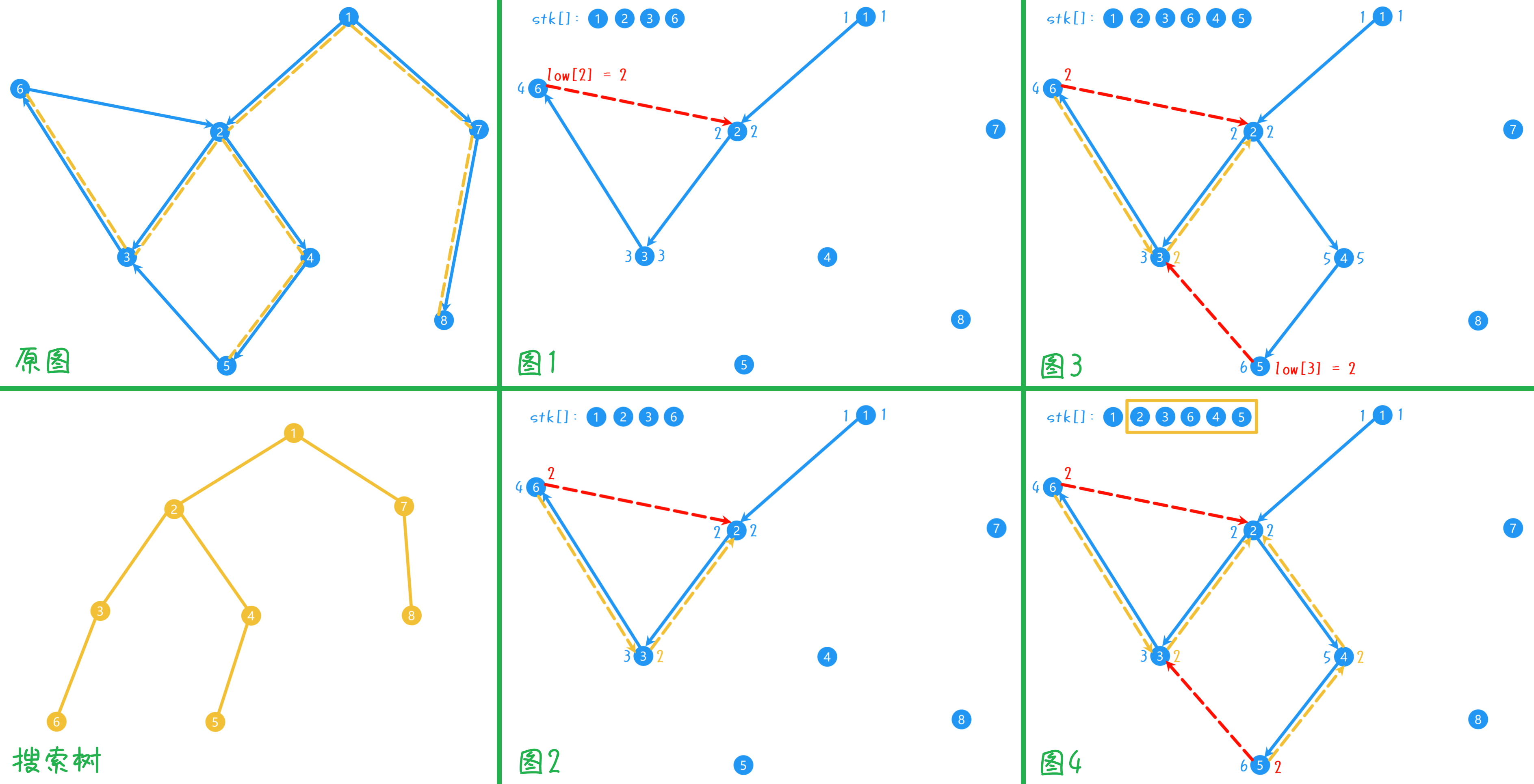
代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; vector<int> g[N]; // 建图 int dfn[N], low[N], idx; // Tarjan 搜索的变量 int col[N], scc; // Tarjan 染色的变量 int stk[N], top; // 维护栈 bitset<N> ins; // 是否入栈 int cnt[N]; // 记录强联通分量大小 // Tarjan 强联通分量,本质是 DFS void Tarjan_SCC(int x) { // 初始化 dfn 和 low dfn[x] = low[x] = ++idx; // 入栈并标记 stk[++top] = x; ins[x] = true; // 处理子节点 for (auto &y : g[x]) { // 如果没走过 dfn[y] = 0,一定是儿子不是回点,先走它,走完递回时用 low[y] 更新 low[x] if (!dfn[y]) { Tarjan_SCC(y); low[x] = min(low[x], low[y]); } // 否则如果是回点:dfn[y] != 0 且 在栈中,向下看一眼并用 dfn[y] 更新 low[x] else if (ins[y]) low[x] = min(low[x], dfn[y]); } // 看自己是不是根,收拢 if (dfn[x] == low[x]) { // 新开一个颜色(计数新的强联通分量) scc++; // 弹出栈并染色,直到 x 也弹出 (top + 1 为了延迟一个点,让 x 本身也被处理) while (stk[top + 1] != x) { col[stk[top]] = scc; // 染色 cnt[scc]++; // 强联通分量大小 +1 ins[stk[top--]] = false; // 弹出栈顶并取消标记 } } } void solve() { int n, m; cin >> n >> m; for (int i = 1; i <= m; i++) { int x, y; cin >> x >> y; g[x].push_back(y); } // 图不保证连通 for (int i = 1; i <= n; i++) // 如果该点没走过,就跑一次 Tarjan if (!dfn[i]) Tarjan_SCC(i); // 存储所有大小 > 1 的强联通分量大小 vector<int> ans; for (int i = 1; i <= scc; i++) if (cnt[i] > 1) ans.push_back(cnt[i]); // 输出答案 if (ans.size()) { sort(ans.begin(), ans.end()); for (auto &a : ans) cout << a << ' '; } else cout << -1 << '\n'; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Tarjan 割点割边
Tarjan 割点割边
1、割点割边:输入点数 $n$ 和边数 $m$ ($n,m \leq 2 \times 10^5$),对于每条边,给出 $x, y$ 表示存在一条 $x$ 到 $y$ 的双向边。输出图中的割点数量和割边数量
2、判断割点:如果一个点在搜索树中有两个及以上的不回子节点(独立子节点),即假如把该节点看作根,其至少有两串子树互相不可到达(在图中,非根节点向上的父亲链连通的部分也可以看作子树),该点即为割点。例如有 $1 - 2 - 3 - 4 - 5 - 3$ 五条无向边:节点 $2$ 有子树 $1$ 和子树 $3$ 互相不可到达,是一个割点;节点 $3$ 有子树 $2$ 和子树 $4$ 互相不可到达($5$ 只是回到 $3$,没有连通 $3$ 之上的节点),是一个割点;而节点 $4$ 的两棵子树 $3$ 和 $5$ 有连通,所以不是割点
3、实现上,先前的 Tarjan SCC 可以将图缩边,判断出完全相通的部分,所以只需要在先前代码修改。对于非根节点 $x$,只需要找到一个子节点 $y$ 使 $low[y] \geq dfn[x]$ 便是割点(只要 $x$ 有一串向下的子树 $y$ 不能回到上面父节点子树,即条件中 $y$ 只能回到 $x$ 自己及以下,就有了两串互相不可到达的子树);对于根节点,就需要两个子节点满足条件。由于不需要求强联通分量,所以不需要染色和栈。此外注意,在无向图上 DFS 一定要判父节点,不能往回走
4、判断割边:与割点几乎相同,不同的是,在从 $x$ 向下走一条边时,如果相连的节点 $y$ 的子树连 $x$ 自己都回不到,就是一条割边。所以只要满足 $low[y] \gt dfn[x]$ 就是割边,不需要判断不回子节点个数代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; vector<int> g[N]; // 建图 int dfn[N], low[N], idx; // Tarjan 搜索的变量 int cut, bri; // 记录割点和割边数量 // Tarjan 割点,如果 fa = 0 那么 x 是根 void Tarjan_Cut(int x, int fa) { // 初始化 dfn 和 low dfn[x] = low[x] = ++idx; int child = 0; // 记录不回子节点个数 // 处理子节点 for (auto &y : g[x]) { // 不走父亲 if (y == fa) continue; // 如果没走过就走,走完递回时用 low[y] 更新 low[x] if (!dfn[y]) { Tarjan_Cut(y, x); low[x] = min(low[x], low[y]); child += (low[y] >= dfn[x]); // 满足不回子节点条件,就记录 +1 } // 只判断是否有回点不求强联通分量,不需要判断栈 else low[x] = min(low[x], dfn[y]); } // fa == 0 是根需要 2 个,fa != 0 只需要 1 个,是割点 if ((!fa && child >= 2) || (fa && child >= 1)) cut++; } // Tarjan 割边,如果 fa = 0 那么 x 是根 void Tarjan_Bri(int x, int fa) { // 初始化 dfn 和 low dfn[x] = low[x] = ++idx; // 处理子节点 for (auto &y : g[x]) { // 不走父亲 if (y == fa) continue; // 如果没走过就走,走完递回时用 low[y] 更新 low[x] if (!dfn[y]) { Tarjan_Bri(y, x); low[x] = min(low[x], low[y]); bri += (low[y] > dfn[x]); // y 回不到 x 及父亲树上,记录割边 } // 只判断是否有回点不求强联通分量,不需要判断栈 else low[x] = min(low[x], dfn[y]); } } void solve() { int n, m; cin >> n >> m; for (int i = 1; i <= m; i++) { int x, y; cin >> x >> y; g[x].push_back(y); g[y].push_back(x); } // 求割点,图不保证连通 for (int i = 1; i <= n; i++) // 如果该点没走过,就跑一次 Tarjan if (!dfn[i]) Tarjan_Cut(i, 0); // 重置 dnf, low, idx for (int i = 1; i <= n; i++) dfn[i] = low[i] = 0; idx = 0; // 求割边,图不保证连通 for (int i = 1; i <= n; i++) // 如果该点没走过,就跑一次 Tarjan if (!dfn[i]) Tarjan_Bri(i, 0); cout << cut << ' ' << bri; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Tarjan 找环
Tarjan 找环
1、找环:输入样例组数 $T$ ($T \leq 10^3$)。每组样例,输入点数和边数 $n$ ($n \leq 2 \times 10^5$),对于每条边,给出 $x, y$ 表示存在一条 $x$ 到 $y$ 的双向边。图中不含重边与自环,可以证明图中有且仅存在一个环,输出环的大小
2、无向图找环,同样用求强联通分量的方式,在求无向图强联通分量过程中转换成有向图,在向下 DFS 的过程中,由于不会向回走父节点,会赋予边一个方向。$n$ 点 $n$ 边的图,求强联通分量一定会求到环,其余大多强联通分量大小为 $1$,如果遇到不为 $1$ 的即为环的大小代码实现
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; vector<int> g[N]; int dfn[N], low[N], idx; int stk[N], top; bitset<N> ins; int ans; // Tarjan 找环 void Tarjan_Cir(int x, int fa) { dfn[x] = low[x] = ++idx; stk[++top] = x; ins[x] = true; // 处理子节点 for (auto &y : g[x]) { if (y == fa) continue; if (!dfn[y]) { Tarjan_Cir(y, x); low[x] = min(low[x], low[y]); } else if (ins[y]) low[x] = min(low[x], dfn[y]); } // 当前点是根 if (low[x] == dfn[x]) { int cnt = 0; // 记录大小 // 出栈记录大小 while (stk[top + 1] != x) { cnt++; ins[stk[top--]] = false; } // 大小 > 1 的强联通分量即为环的大小 if (cnt > 1) { ans = cnt; return; } } } void solve() { int n; cin >> n; // 初始化,置空清零 for (int i = 1; i <= n; i++) { g[i].clear(); stk[i] = dfn[i] = low[i] = 0; ins[i] = false; } stk[n + 1] = 0; ans = idx = top = 0; for (int i = 1; i <= n; i++) { int x, y; cin >> x >> y; g[x].push_back(y); g[y].push_back(x); } // 一定有环,图一定连通 Tarjan_Cir(1, 0); cout << ans; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; cin >> T; while (T--) solve(); return 0; }



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试