双指针 | 山暮云秋

同向双指针-滑动窗口

例题引入

1、给定一个已知序列且数组元素都是正数(例如 $\{2, 3, 1, 2, 4, 3\}$)，再给定一个 $target$(例如 $7$)，从中找出最短的一个子序列，使子序列的和 $\geq target$，输出最短子序列的长度
2、普通的暴力做法是两层循环分别枚举子序列的左右端点，显然这样的时间复杂度为 $O(n^2)$，运行速度很慢
3、另一种思路是使用双指针：由于数组元素都是正数，因此当子序列向右延伸时和一定递增。我们先以 $[0, 3]$ 为第一个子序列，和为 $8$；向右移动左指针，发现 $[1, 3]$ 和为 $6$ 不满足条件，便向右移动右指针指向 $[1, 4]$ ，和为 $10$；继续向右移动左指针，发现 $[2, 4]$ 和为 $7$ 满足条件；以此类推直至末尾。最终发现最短子序列是 $[4, 5]$ 长度为 $2$
4、这种思路下，左右指针都不需要向左回退，因此两个指针都最多只需要遍历一次数列，时间复杂度为 $O(n)$

代码实现

#include <iostream>
using namespace std;

int arr[100001];

int main()
{
    int n, target;
    cin >> n >> target;
    for (int i = 0; i < n; i++)
        cin >> arr[i];

    int L = 0, R = 0;                  // 左右指针
    int sum = arr[R], ans_min = n + 1; // 初始化 sum 和 ans，sum 为 arr[R] 的值，ans_min 为整个序列的长度 +1
    // 双指针：以左指针作为基准向右推进
    while (L < n)
    {
        // 如果右指针没有到尽头，且当前和不够
        while (R < n && sum < target)
        {
            // 移动右指针
            R++;
            sum += arr[R];
        }

        // 如果满足条件(为了防止到尽头仍然和不够)
        if (sum >= target)
            ans_min = min((R - L + 1), ans_min); // 更新子序列最小值

        // 移动左指针
        sum -= arr[L];
        L++;
    }

    // 如果 ans_min 没有改变，说明整个序列的和都不满足要求，输出 -1
    if (ans_min == n + 1)
        cout << "-1";
    else
        cout << ans_min;
    return 0;
}

相向双指针-三数之和

两数之和

1、给定一个升序排列的序列(例如 $\{2, 3, 4, 6, 8\}$)，再给定一个 $target$(例如 $9$)，从序列中找出两个数，满足它们的和 $= target$，输出这两个数
2、简单推测可得，暴力枚举的时间复杂度为 $O(n^2)$ ，而使用双指针只需要 $O(n)$
3、因为数列是升序的，所以我们先从两端开始(左指针指向最左，右指针指向最右)。如果两指针之和大于目标值，由于升序排列，说明右指针值加上任意一个左指针向右的值都会大于目标，应当让右指针向左移动；相对的，如果两指针之和小于目标值，说明左指针值加上任意一个右指针向左的值都会小于目标，应当让左指针向右移动。以此类推，直到找到目标或者两指针重叠

代码实现

#include <iostream>
using namespace std;

int arr[100001];

int main()
{
    int n, target;
    cin >> n >> target;
    for (int i = 0; i < n; i++)
        cin >> arr[i];

    bool flag = true;
    int L = 0, R = n - 1;
    while (L < R)
    {
        if (arr[L] + arr[R] > target)
        {
            R--;
            continue;
        }
        else if (arr[L] + arr[R] < target)
        {
            L++;
            continue;
        }
        else
        {
            cout << arr[L] << " " << arr[R] << endl;
            flag = false;
            break;
        }
    }

    if (flag)
        cout << "-1";
    return 0;
}

三数之和

1、给定一个升序排列的序列(例如 $\{-4, -1, -1, 0, 1, 2\}$)，是否存在子序列 $\{arr[i], arr[j], arr[k]\}$ 满足 $i \not= j \not= k$ 且三数之和 $= 0$，子序列元素顺序不重要，输出满足条件的所有不重复的子序列
2、因为元素顺序不重要，即 $\{-1, 0, 1\}$ 和 $\{1, -1, 0\}$ 是相同答案，我们可以规定 $i \lt j \lt k$ 。$i$ 作为最左侧的数，通过遍历(范围 $[0, n-2)$)得到，$j$ 和 $k$ 采取上面两数之和的方式，用双指针来快速判断
3、需要注意，输出需要避免重复，则下标为 $1$ 和 $2$ 的 $-1$ 可以看作同一组判断，因此可以跳过一组避免重复($j$ 和 $k$ 也同理)。此外，对于优化而言：如果序列当前 $i$ 对应值与后两个相邻数之和 $\gt 0$，那么向后整个序列再任取两个数之和都会 $\gt 0$ ；如果当前 $i$ 对应的值与最后两个数之和 $\lt 0$ ，那么这轮的 $i$ 再任取两个数之和都会 $\lt 0$

代码实现

#include <iostream>
using namespace std;

int arr[100001];

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> arr[i];

    bool flag = true;
    int i, j, k, sum;
    // 遍历最左侧的数 i
    for (i = 0; i < n - 2; i++)
    {
        // 如果这一次判断与上一次判断是同一组判断，则跳过
        if (i > 0 && arr[i] == arr[i - 1])
            continue;
        // 当前 i 对应值与后两个相邻数之和大于 0，则向后整个序列任取两个数都大于 0，且之后 arr[i] 只会更大，所以 break
        if (arr[i] + arr[i + 1] + arr[i + 2] > 0)
            break;
        // 当前 i 对应值与最后两个数之和小于 0，则这轮 i 任取两个数都小于 0，但之后 arr[i] 还可能变大，所以 continue
        if (arr[i] + arr[n - 1] + arr[n - 2] < 0)
            continue;

        // 这一轮 i 的 j(左指针) 和 k(右指针)
        j = i + 1;
        k = n - 1;
        while (j < k)
        {
            sum = arr[i] + arr[j] + arr[k];
            if (sum > 0)
                k--;
            else if (sum < 0)
                j++;
            else
            {
                cout << arr[i] << " " << arr[j] << " " << arr[k] << endl;
                flag = false;

                // 改变 j 和 k，并且跳过重复的判断
                j++;
                while (j < k && arr[j] == arr[j - 1])
                    j++;
                k--;
                while (k > j && arr[k] == arr[k + 1])
                    k--;
            }
        }
    }

    if (flag)
        cout << "-1";
    return 0;
}

相向双指针-接雨水

盛水最多的容器

1、给定一个数列(例如 $\{1, 8, 6, 2, 5, 4, 8, 3, 7\}$)，数列的每个数表示对应位置竖线的高度，找出两条竖线，使竖线与 x 轴构成的容器的容积最大，输出最大的容积
2、由题意可知，容器的容积与较短的线长和两线的距离有关。试分析，随便选择两条线，看较短的线，如果短线和两者之间的线构成容器的话：任选之间的线比短线短，容器的宽度高度都变小，容积变小；任选之间的线比短线长或等于短线，容器的宽度变小高度不变，容积变小。由此证明，短线和之间的任何线都无法构成一个容积更大的容器，则如果要找到容积更大的容器，就一定不包含这条短线，可以直接舍掉，在剩下的线中寻找
3、我们令双指针分别指向左右边界，由刚才的证明可知，我们只需要移动较短的线的指针，每轮计算容积，如果比先前结果大，就更新结果，直到两指针重叠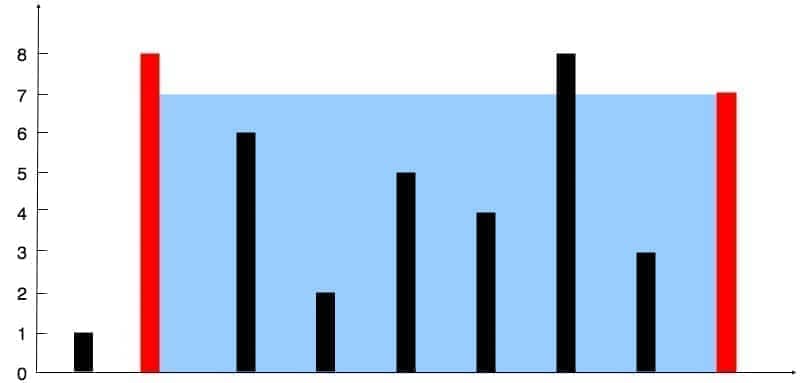

代码实现

#include <iostream>
using namespace std;

int arr[100001];

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> arr[i];

    int L = 0, R = n - 1, V, ans = 0;
    while (L < R)
    {
        V = (R - L) * min(arr[L], arr[R]);
        ans = max(ans, V);

        // 移动较短的线的指针
        if (arr[L] < arr[R])
            L++;
        else
            R--;
    }
    cout << ans;
    return 0;
}

接雨水

1、给定一个数列(例如 $\{0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1\}$)，数列的每个数表示对应位置宽度为 1 的柱子的高度，计算这样排列的柱子下雨能接多少雨水，输出答案。对此问题，给出如下思路，并且可以针对该思路使用双指针进行优化
2、我们假设每一数列都有一个桶(如红色所示)，桶的左木板高度取决于左边的最大高度，而右木板高度取决于右边的最大高度，因此我们可以分别计算前缀最大值和后缀最大值。因为桶所能接的水取决于较短的木板高度，因此同一位置的前缀最大值和后缀最大值的较小值便是桶能接的水的容量，再减去当前位上柱子所占的容量，就得到了当前位的答案
3、这样的代码时间复杂度为 $O(n)$ ，已经十分优秀了，但空间复杂度也为 $O(n)$ ，仍然可以优化。假设我们只知道红色部分的前缀最大值和后缀最大值，如果我们想要计算右侧的桶(绿色)，只知道右侧木板长为 $3$ ，左侧具体多长并不知道，无法计算容量；但如果我们计算左侧的桶(蓝色)，左侧木板长为 $1$ ，但右侧木板至少长为 $3$ ，便可以算出容量(就是前缀最大值)。然后，便可以继续向下计算前缀最大值，以此类推
4、优化总结：如果前缀小于后缀，那么左边木桶的容量就是前缀最大值；如果后缀小于前缀，那么右边木桶的容量就是后缀最大值。通过使用双指针分别指向左右边界，再按照刚才的步骤模拟即可，这样优化的程序空间复杂度只有 $O(1)$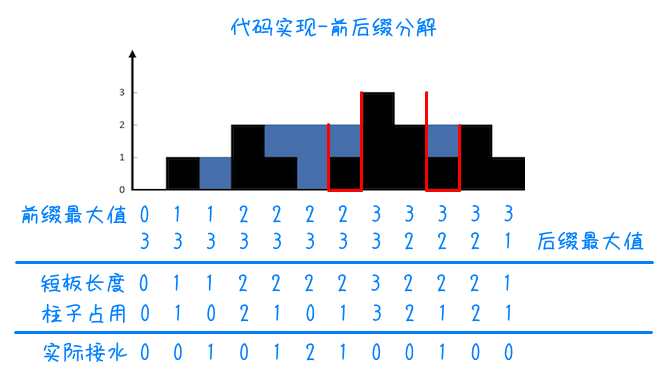

代码实现-前后缀分解

#include <iostream>
using namespace std;

int arr[100001], pre_max[100001], suf_max[100001];

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> arr[i];

    // 计算前缀最大值和后缀最大值
    pre_max[0] = arr[0];
    suf_max[n - 1] = arr[n - 1];
    for (int i = 1; i < n; i++)
    {
        pre_max[i] = max(pre_max[i - 1], arr[i]);
        suf_max[n - i - 1] = max(suf_max[n - i], arr[n - i - 1]);
    }

    int ans = 0;
    for (int i = 0; i < n; i++)
        ans += min(pre_max[i], suf_max[i]) - arr[i];
    cout << ans;
    return 0;
}

代码优化-相向双指针

#include <iostream>
using namespace std;

int arr[100001];

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> arr[i];

    int L = 0, R = n - 1, ans = 0;
    int pre_max = 0, suf_max = 0; // 在循环中一边更新左右指针，一边更新最大值

    // 不用 <= 是因为当 L == R 时一定在最高点相遇，不可能接水
    while (L < R)
    {
        // 更新最大值
        pre_max = max(pre_max, arr[L]);
        suf_max = max(suf_max, arr[R]);

        // 如果前缀小于后缀，那左边木桶的容量就知道了
        if (pre_max < suf_max)
        {
            ans += pre_max - arr[L]; // 能接的水就是前缀最大值 - 柱子容量
            L++;
        }
        // 否则后缀小于前缀(等于也可以)，那右边木桶的容量就知道了
        else
        {
            ans += suf_max - arr[R]; // 能接的水就是后缀最大值 - 柱子容量
            R--;
        }
    }
    cout << ans;
    return 0;
}

同向双指针-滑动窗口

相向双指针-三数之和

相向双指针-接雨水

页底评论