Prim 最小生成树(朴素)
生成树 与 MST
1、在无向连通图中,找出一个节点最多的子连通图(有 $n$ 个点,$n-1$ 条边),这样的子连通图一定是树,称为生成树。最小生成树指各边权值之和最小的生成树,称为 MST(Minimum Spanning Tree)
2、如下图,便是一幅无向连通图,该图的最小生成树为图中红色所示的子连通图(有 $5$ 个点,$4$ 条边),其权值和为 $10$
3、对于最小生成树的生成,可以通过基于点的 Prim 最小生成树与基于边的 Kruskal 最小生成树完成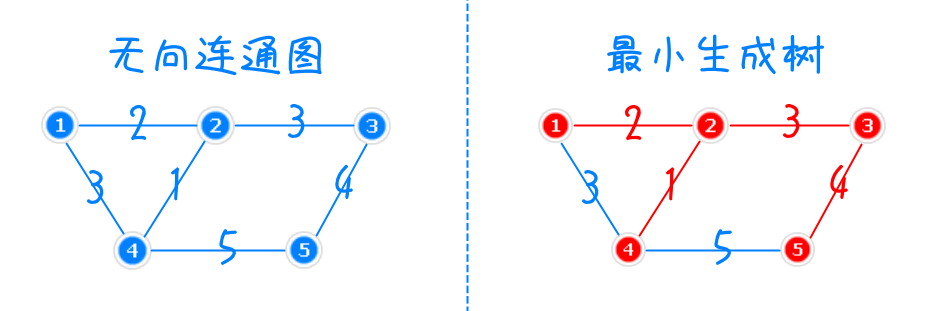
Prim 最小生成树(朴素)
1、最小生成树:给定 $n$ 个点 $m$ 条边($n \leq 10^5$)的无向图,对于 $m$ 条边,每次输入 $u、v、w$,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的边。输出其最小生成树的权值之和,如果没有则输出 $-1$
2、Prim 最小生成树通过假想 $inTree$ 标识在树内的点,通过 $d[i]$ 维护点 $i$ 到 $inTree$ 的最近距离,每次将 $d[i]$ 最小的点纳入 $inTree$,直到所有点都在 $inTree$ 内完成生成。在实际实现中,通过 $inTree[i]$ 来标识 $i$ 在 $inTree$ 内,且设置 $d[i] = 0$
3、其思路如下图:起始,初始化 $d[]$ 为无穷;任选一点作为起点,此处$1$ 为起点,标记 $d[1] = 0$ (在 $inTree$ 内),更新 $inTree$ 相邻的点(即 $2,3$)的 $d[i]$ (取较小值),此处不需要更新点 $4,5$ 是因为 $inTree$ 的相邻点 $2, 3$ 一定比他们更近;将 $d[i]$ 最小的点纳入 $ inTree$ ($d[2] = 0$),再次更新附近的 $d[i]$ ,注意此时 $d[4] = min(1, 3) = 1$ ;以此类推,循环操作,直至生成树完成。操作后,如果有任何点不在 $inTree$ 中,说明不存在生成树
4、在此通过邻接矩阵实现朴素算法,这种写法并不与上面思路完全相同。由于朴素算法只能处理较小范围数据,所以还不能完成该题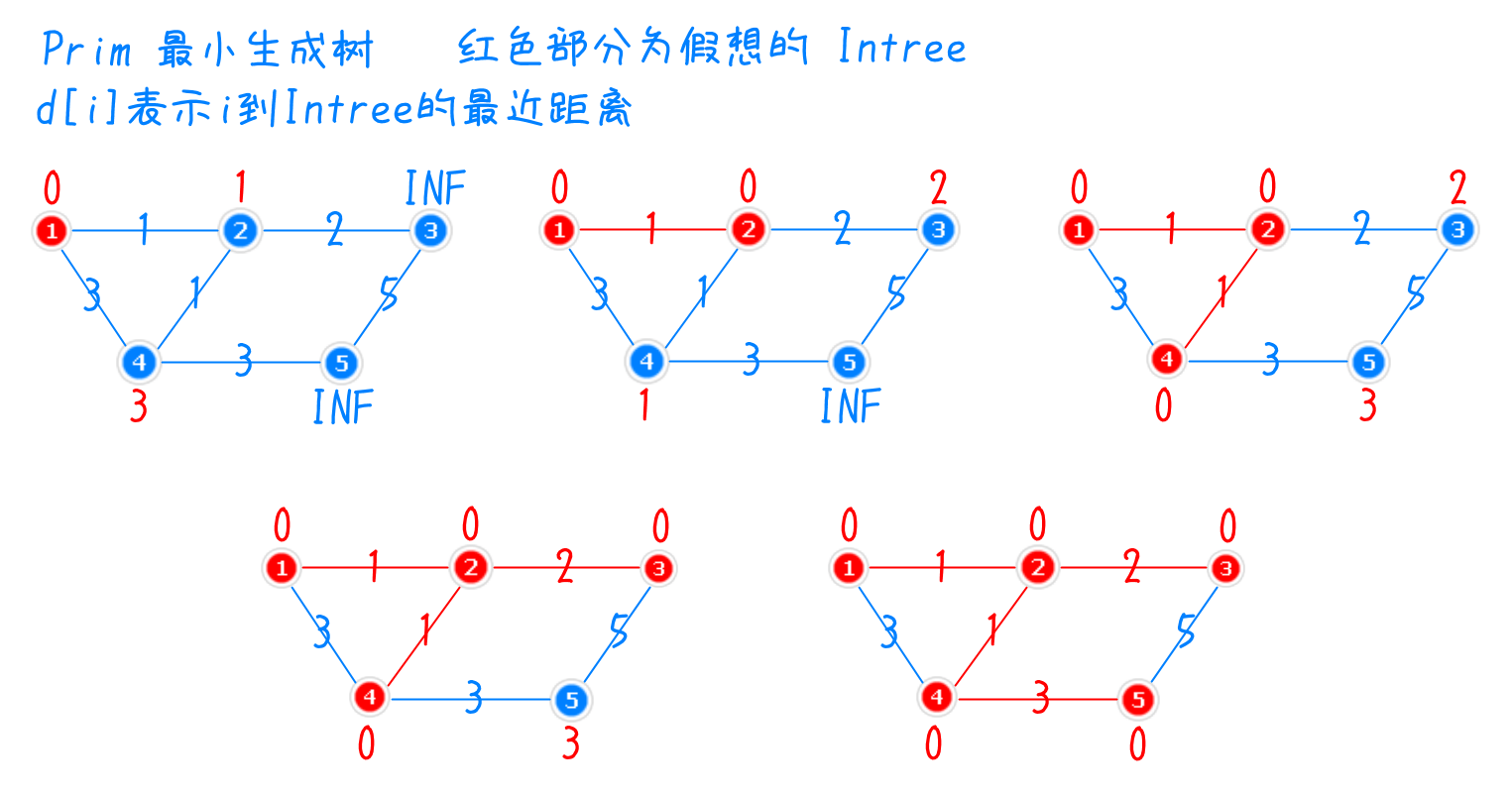
代码实现
#include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f3f; const int N = 1e3 + 10; int a[N][N], d[N]; // a 为无向图,d 为最短路径 int n, m, ans = 0; bitset<N> inTree; // Prim 朴素 void Prim() { // 初始化 d[] memset(d, INF, sizeof(d)); // 初始化:把 1 作为起点,计入 inTree,更新附近点的 d[j] d[1] = 0; inTree[1] = true; for (int j = 2; j <= n; j++) d[j] = min(d[j], a[1][j]); // 更新 1 到 j 的距离 d[j] // 还需 n-1 次操作(去除了起点) for (int i = 1; i < n; i++) { // 查找 d[i] 最小的点 u int u = 1; for (int j = 1; j <= n; j++) if (inTree[u] || (!inTree[j] && d[j] < d[u])) u = j; // 计入答案,u 点纳入 inTree ans += d[u]; inTree[u] = true; d[u] = 0; // 更新 u 附近的 d[j],因为只将 u 纳入了 Intree,即只有 u 周围的点的 d[j] 可能有变动 for (int j = 1; j <= n; j++) { if (inTree[j]) // 已经在 inTree 的不需要处理 continue; d[j] = min(d[j], a[u][j]); // 将 u 到 j 这条变动的新路距离 与 原先的 d[j] 取短 } } // 如果有任何点不在 inTree 中,说明不存在生成树 for (int i = 1; i <= n; i++) if (!inTree[i]) ans = -1; } void solve() { cin >> n >> m; // 初始化 d,并设置自环为 0 memset(a, INF, sizeof(a)); for (int i = 1; i <= n; i++) a[i][i] = 0; // 存储无向图 for (int i = 1; i <= m; i++) { int u, v, w; cin >> u >> v >> w; // 重边取短值 a[u][v] = min(a[u][v], w); a[v][u] = min(a[v][u], w); } Prim(); cout << ans; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Prim 最小生成树(堆优化)
Prim 最小生成树(堆优化)
1、最小生成树:给定 $n$ 个点 $m$ 条边($n \leq 10^5$)的无向图,对于 $m$ 条边,每次输入 $u、v、w$,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的边。输出其最小生成树的权值之和,如果没有则输出 $-1$
2、对于朴素算法中,查找 $d[i]$ 最小的点这一步可以通过优先队列维护($w$ 的小根堆);在更改 $d[j]$ 时,如前所述思路中提到,只需要更改相邻点的 $d[j]$ ,而邻接矩阵却进行了大量无用查找,可以改为邻接表建图,更改时只需要遍历出边优化代码实现
#include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f3f; const int N = 1e5 + 10; struct Edge { // x 为出点,w 为权值 int x, w; }; // 重载 < 运算,用于优先队列的 < 规则 bool operator<(const Edge &u, const Edge &v) { // 注意:优先队列通过 < 成立得到大根堆,所以需要小根堆则在比较中应使用 > 比较 // 用 > 比较 w,保证堆顶元素 w 最小(d[i] 最小) return u.w > v.w; } vector<Edge> g[N]; // 邻接表建图,g[] 为 vector<Edge> 的数组 int d[N]; // d[] 为最短路径 int n, m, ans = 0; bitset<N> inTree; // Prim 堆优化 void Prim() { // 初始化 d[] memset(d, INF, sizeof(d)); d[1] = 0; // 优先队列,需要提前定义 Edge 的 < 规则,小根堆 priority_queue<Edge> pq; // pq 中的 w 即为 d[x] pq.push({1, d[1]}); // 把点 1 作为起点,入队 // 只要队列不为空 while (!pq.empty()) { // 取出 d[i] 最小的点的 x,并弹出 int x = pq.top().x; pq.pop(); // x 已入树则跳过 if (inTree[x]) continue; // 将 x 入树 inTree[x] = true; ans += d[x]; d[x] = 0; // 更新 x 附近的 d[],遍历 x 的出边 for (auto &[y, w] : g[x]) { // 这种写法,注意此时 d[x] = 0,出边如果没入过队 d[y] 都为无穷 // 所以判断 d[x] + w < d[y] 可以简写为 w < d[y],只要 d[y] 需要被更改,y 便可能是下一条边 if (!inTree[y] && w < d[y]) { d[y] = w; // 更新 d[y] pq.push({y, d[y]}); // 点 y 入队 } } } // 如果有任何点不在 inTree 中,说明不存在生成树 for (int i = 1; i <= n; i++) if (!inTree[i]) ans = -1; } void solve() { cin >> n >> m; // 存储无向图 for (int i = 1; i <= m; i++) { int u, v, w; cin >> u >> v >> w; // 重边没有消除,但在优先队列中,会自动取 w 最小的 g[u].push_back({v, w}); g[v].push_back({u, w}); } Prim(); cout << ans; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }
Kruskal 最小生成树
Kruskal 最小生成树
1、最小生成树:给定 $n$ 个点 $m$ 条边($n \leq 10^5$)的无向图,对于 $m$ 条边,每次输入 $u、v、w$,表示存在一条从 $u$ 到 $v$ 的权值为 $w$ 的边。输出其最小生成树的权值之和,如果没有则输出 $-1$
2、Kruskal通过贪心的思想选边,是基于边的最小生成树,思路如下:将所有边升序排列,按照从小到大选边;如果该边两点已经连通(在同一连通块),则跳过;否则选择该边,并将两点连通。操作后,如果有任何点不属于同一连通块,说明不存在生成树
3、该思想需要使用并查集来维护连通关系。由于生成树不存在环,而在同一连通块中的两点连线一定会形成环,所以一定不成立,以此来判断是否选边代码实现
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 10; struct Edge { // u 到 v 权值为 w 的边 int u, v, w; }; bool operator<(const Edge &lhs, const Edge &rhs) { // 按照 w 升序 return lhs.w < rhs.w; } int n, m, ans = 0; vector<Edge> es; // 存储所有边信息 int pre[N]; // 并查集 // 初始化函数 void init(int n) { for (int i = 0; i <= n; i++) pre[i] = i; } /* 并查集的操作 */ // 路径压缩的 root() int root(int u) { return pre[u] = (pre[u] == u ? u : root(pre[u])); } // 合并操作 void merge(int u, int v) { pre[root(u)] = root(v); } // 查找操作 bool isCon(int u, int v) { return root(u) == root(v); } // Kruskal 算法 void Kruskal() { init(n); // 初始化并查集 sort(es.begin(), es.end()); // 按 w 升序排列 // 按顺序遍历所有边 for (auto [u, v, w] : es) { // 如果 u v 在同一连通块,跳过 if (isCon(u, v)) continue; // 选择当前边,连通 u v ans += w; merge(u, v); } // 所有点都应在同一连通块,如果有任何点不属于同一连通块,说明不存在生成树 for (int i = 2; i <= n; i++) { if (!isCon(i, 1)) ans = -1; } } void solve() { cin >> n >> m; // 存储无向图 for (int i = 1; i <= m; i++) { int u, v, w; cin >> u >> v >> w; es.push_back({u, v, w}); } Kruskal(); cout << ans; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T = 1; // cin >> T; while (T--) solve(); return 0; }



如果较为紧急,建议添加微信或QQ,并注明来意
评论系统可能加载较慢,请耐心等待或刷新重试