贪心算法

适用前提

1、简言之：可以找到一个局部最优解；可以从局部最优解推广到全局最优解
2、严谨地说，两个条件分别是最优子结构和贪心选择性质
3、一般来说，贪心法往往是将某个东西排序，或者用堆(优先队列)等数据结构，每一步都取局部最优解，进而得到全局最优解
分析步骤

1、确定要贪的东西和贪心策略(根据什么来贪心)。例如某个东西的性价比，优先选性价比高的；或者某个区间，按照左端点还是右端点排序等
2、从局部特殊情况出发，简单分析使用贪心策略是不劣的。即大致确定使用贪心，一定不比其他方法更差
3、一般来说，大多数能贪心的东西，对答案的贡献都相等。比如背包问题，如果每件物品体积都相等，那肯定选择性价比优先。当有多种选择时，但它们对答案的贡献相等时，优先选择开销小的，或能给后面留下更多选择空间的
4、开始贪心，得到问题的解

小 e 看电视

小 e 看电视

1、小 e 看电视(链接失效)：简单描述，现在给出一些区间，问最多能选出多少个区间且它们互不重叠
2、首先考虑特殊情况。当右端点相等时，如下图 $1-4$ 中，能发现选任意一个区间对答案的贡献都一样为 $1$(因为在右端点相同的区间中只能选出一个，其余必然与之重叠)；在此基础上增加 $5$ 和 $6$ 两个区间，则 $1-5$ 之间更应当选择前四者，这样实际剩余的选择空间为黄色部分(还可以选择 $6$)；而如果选择 $5$，则实际剩余选择空间为橙色部分(无法选择 $6$)。因此第一个贪心原则：先选右端点较小的，剩余选择空间较大，即右端点升序
3、在右端点相同的基础上，还有特殊情况。当出现长度为 $0$ 的区间时，如下图，图中红色部分表示由于从选择的左端点开始而不能选择的部分。按照左侧选择 $1$ 时，在 $1$ 结束后还可以选择 $2$、$3$、$4$；按照右侧选择 $1$ 时，由于 $1$ 的左端点的开始位置靠后，所以 $1$ 结束后不能选择 $4$、$5$，只能选择 $2$、$3$。因此第二个贪心原则：右端点相同时，选左端点较小的，剩余选择空间较大，即左端点也升序
4、此时，按照两个贪心原则写出代码即可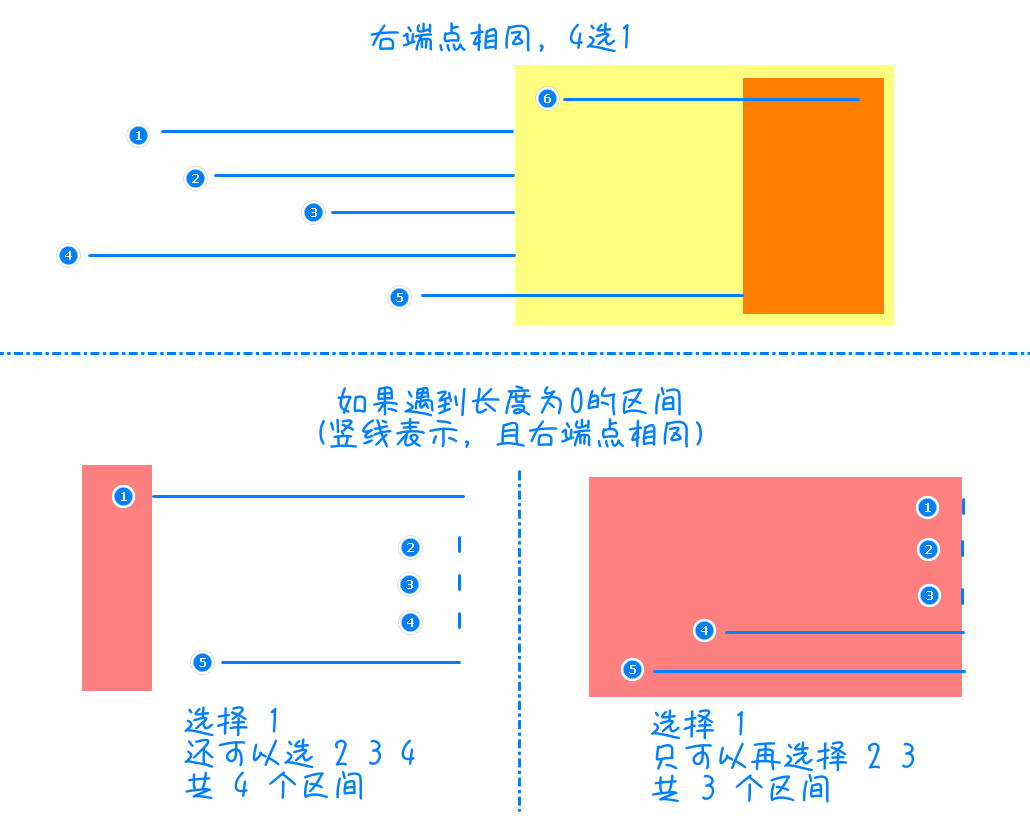

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10, T = 20;

// 用结构体存储区间
struct Node
{
        int l, r;
} node[N];

// 用于 sort 的比较函数
bool comp(Node u, Node v)
{
    // 如果右端点相同，按照左端点升序
    if (u.r == v.r)
        return u.l < v.l;

    // 按照右端点升序
    return u.r < v.r;
}

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> node[i].l >> node[i].r;

    // 排序，按照右端点升序，在此基础上再按照左端点升序
    sort(node, node + n, comp);

    // now 表示当前时间，ans 记录答案
    int now = 1, ans = 0;
    for (int i = 0; i < n; i++)
    {
        // 如果该区间的左端点已经过去，则跳过
        if (node[i].l < now)
            continue;
        // 记录当前区间右节点为当前时间，答案计数 +1
        now = node[i].r;
        ans++;
    }
    cout << ans << endl;
    return 0;
}

排队取水问题

排队取水问题

1、排队取水问题(链接失效)：有 n 个人，m 个窗口，每人需要到窗口打饭，所需时间各不相同，如何安排可以使得所有人等待时间之和最小
2、由于每人进入窗口排队的等待时间，相当于先前排队的人的所需时间，即放的越早的，会被越多的人等待。又因为排队没有顺序要求，所以可以先按照时间升序排列，再进行分配
3、每次都分配下一位去往当前状态最空闲(等待时间最短)的窗口，这样确保了每人的等待时间最短，窗口的维护可以用堆来实现

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;
long long a[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        cin >> a[i];
    sort(a, a + n); // 升序排列

    // 创建优先队列(堆)，小根堆(使用 > 号)
    priority_queue<long long, vector<long long>, greater<long long>> pq;
    // 初始化堆，有 m 个窗口，放 m 个 0 进入堆
    for (int i = 0; i < m; i++)
        pq.push(0);

    long long ans = 0;
    // 分配排队
    for (int i = 0; i < n; i++)
    {
        long long x = pq.top(); // 取出等待时间最小的窗口，x 为其需要的等待时间
        pq.pop();               // 先抹去等待时间最小的窗口(稍后添加回来)
        pq.push(x + a[i]);      // 将 x + a[i] 重新加入堆
        ans += x;
    }

    cout << ans << endl;
    return 0;
}

贪心算法

小 e 看电视

排队取水问题

页底评论