二分枚举 | 山暮云秋

二分查找

引入

1、假设对于一个有序数列，例如 $\{1, 2, 3, 5, 5, 5, 8, 9\}$ (实际可能会很长)，我们要在里面查找某个元素的位置或其是否存在
2、如果普通地使用循环遍历，那么时间复杂度为 $O(n)$ 常数级；但如果使用二分查找，时间复杂度仅为 $O(\log_2 n)$ 对数级，效率大大提升
3、二分查找每次操作得到当前未比较序列的中间下标 $mid$，如果 $mid$ 对应的值满足(或不满足)条件，则对于有序数列而言，$mid$ 前面的一系列值都满足(或都不满足)条件，这样便一次查找了未比较序列的一半的元素，便可根据情况调整未比较序列的边界。重复以上操作，直到未比较序列都已经比较，整个序列便按照给定的条件分为了(满足条件/不满足条件)两个组别，根据实际情况返回下标即可

左闭右开的写法

1、左闭右开指的是每次查找的未比较序列为 $[L, R)$ ，对于这样的序列，必须满足 $L + 1 \not= R$ 才是合法序列。这种写法是目前较为主流的写法
2、注意二分查找本质上是将序列按照条件分为两组，我们用 $L$ 和 $R$ 标记两组的边界，而具体的条件需要根据需求更改，返回的值也要根据需求调整，因此需要具体分析
3、大致的代码模板如下，需要酌情修改的地方已注释标注说明。下图给出了面对不同要求的调整方法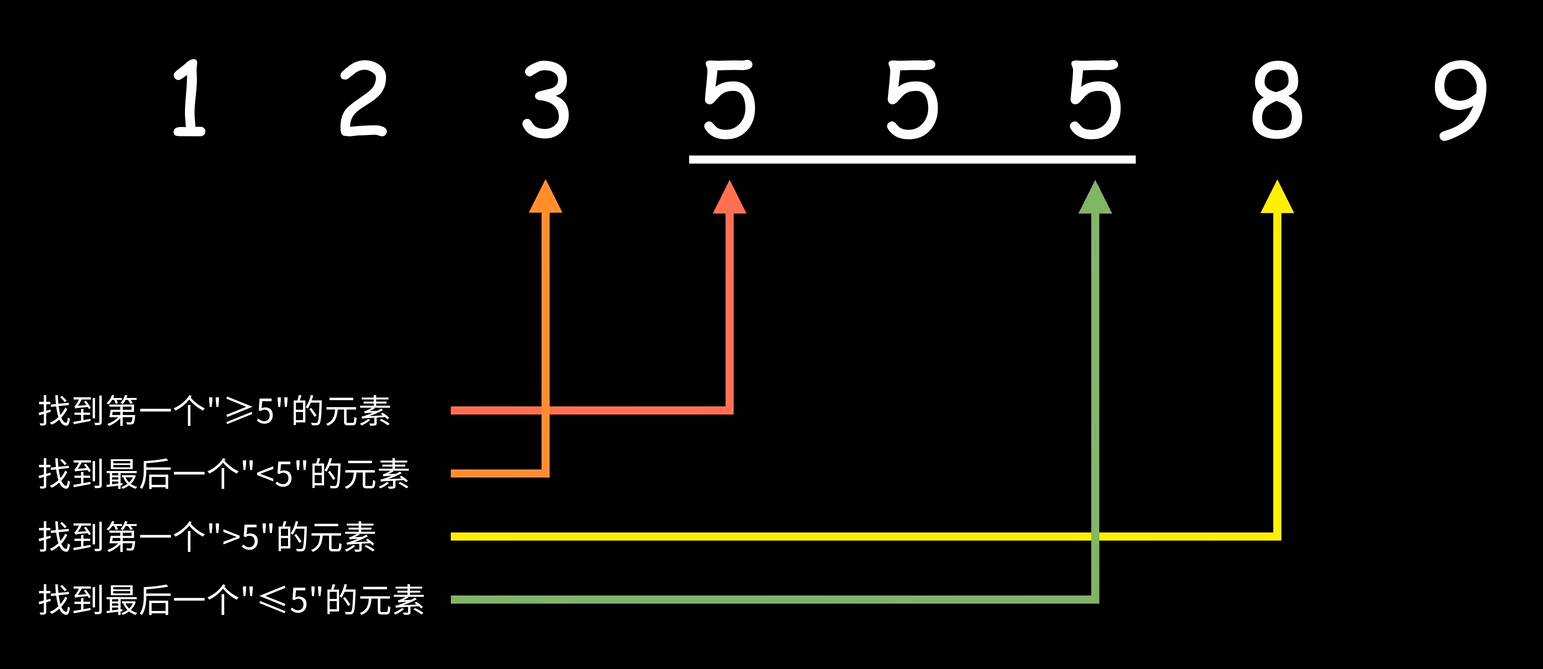

#include <iostream>
using namespace std;

// [L, R) 左闭右开的写法
int binary_search(int arr[], int n, int key)
{
    // L 表示从最左端到下标 L 处都属于 A 组，R 表示从最右端到下标 R 处都属于 B 组
    // L 和 R 都越出边界一个元素，为了应对所有元素都是 A 组或都是 B 组的情况
    int L = -1, R = n;
    int mid;

    // 左闭右开的写法，L 和 R 不能相等，否则 [L, R) 是非法区间。直到二者相邻，则表示 A 组 B 组界限已清晰
    // 注意：这种写法循环条件不可写为 while(L < R)，否则 L = -1, R = 0 会死循环
    while (L + 1 != R)
    {
        mid = (L + R) / 2;  // 计算中间值下标，向下取整
        if (arr[mid] < key) // 属于 A 组的条件，按照实际需要更改!!!
            L = mid;        // 说明从最左端到 mid 都属于 A 组，L 记录 A 组边界到 mid
        else                // 否则说明属于B组
            R = mid;        // 说明从最右端到 mid 都属于 B 组，R 记录 B 组边界到 mid
    }
    // 至此，数列按照 if 的条件分为了 A B 两组，L 和 R分别表示两组的边界下标，根据实际情况返回 L 或 R 或其他下标
    return R;
}

int main()
{
    int arr[8] = {1, 2, 3, 5, 5, 5, 8, 9};
    // 查找第一个 >=5 的下标：函数 if 的条件为 arr[mid] < 5，这些下标将划归 A 组，其余将划归 B 组
    // 函数返回 R，便是返回 B 组第一个元素下标，即第一个 >=5 的元素下标
    cout << binary_search(arr, 8, 5);
    return 0;
}

左闭右闭的写法

#include <iostream>
using namespace std;

// [L, R] 左闭右闭的写法：只返回答案，如果没有找到则返回 -1
int binary_search(int arr[], int n, int key)
{
    int L = -1, R = n;
    int mid;

    while (L <= R)
    {
        mid = (L + R) / 2;

        if (arr[mid] < key)
            L = mid + 1;
        else if (arr[mid] > key)
            R = mid - 1;
        else
            return mid;
    }
    return -1;
}

int main()
{
    int arr[8] = {1, 2, 3, 5, 5, 5, 8, 9};
    cout << binary_search(arr, 8, 5);
    return 0;
}

STL 的二分查找

1、lower_bound()和upper_bound()是STL中的算法，用于对有序序列进行二分查找。其格式为lower_bound(起始位置迭代器, 尾后位置迭代器, 查找值, [可选的自定义规则])，返回值为元素的迭代器
2、在数组为升序的情况下，二者都默认使用小于运算符比较。lower_bound()查找的是不小于(大于等于)给定值的第一个元素的迭代器；upper_bound()查找的是严格大于给定值的第一个元素的迭代器
3、当数组为降序的情况下，必须在第四个参数更改比较规则为大于运算符。lower_bound()会查找不大于(小于等于)给定值的第一个元素的迭代器；upper_bound()会查找严格小于给定值的第一个元素的迭代器
4、善于使用返回值的加减可以实现更多功能，如升序数组的lower_bound() - 1，将指向最后一个小于给定值的元素；升序数组的upper_bound() - 1，将指向最后一个小于等于给定值的元素；以此类推
```
/* 数组升序时 */
vector<int> v = {1, 2, 4, 4, 5, 6};
// it 指向第一个值为 4 的元素
auto it = lower_bound(v.begin(), v.end(), 4);
// it 指向第一个值为 5 的元素
auto it = upper_bound(v.begin(), v.end(), 4);
// key 为第一个值为 4 的元素的下标
int key = lower_bound(v.begin(), v.end(), 4) - v.begin();

/* 数组降序时 */
vector<int> v = {6, 5, 4, 4, 2, 1};
// 使用 lambda 定义规则
auto comp = [](int a, int b) { return a > b; };
// it 指向第一个值为 4 的元素
auto it = lower_bound(v.begin(), v.end(), 4, comp);
// it 指向第一个值为 2 的元素
auto it = upper_bound(v.begin(), v.end(), 4, comp);
// key 为第一个值为 4 的元素的下标
int key = lower_bound(v.begin(), v.end(), 4, comp) - v.begin();
```

二分答案

例题引入

1、在二分查找的基础上，对于数据量在 $10^5$ 以上时，二分答案是一种很常用的算法。如果直接线性处理且时间复杂度达到 $O(n^2)$ 时，程序大概率会超时，而二分答案通常至少能将其优化为 $O(n \log_2 n)$ 对数级
2、在此以木材加工为例。该题本身是一个最值问题，但直接求最值很不好求，但是如果告诉我们切 $5cm$ 一段，变成一个判定问题就比较简单了，二分答案便可以将一个最值问题转换成判定问题
3、但我们并不知道答案是多少，因此我们可以先假设答案的范围为 $[1, 10^9]$ (实际不需要这么大，根据情况分析)。在这个范围内，如果某个数不是答案，那这个数到右边的范围都不是答案；同理如果一个答案可以，那这个数到左边的范围都可以是答案。因此，这种问题便可以对答案进行二分讨论
4、通常当一个问题可以二分答案时，我们需要定义一个check函数用来进行判定，在main中通过二分查找的形式来二分答案

代码实现

#include <iostream>
using namespace std;

// 原木的数量 和 需要切成小段的数量
int n, k;
int len[100001];

// 判断答案是否成立
bool check(int mid)
{
    long long ct = 0;

    if (mid == 0) // 防止除数为 0
        return false;

    for (int i = 0; i < n; i++)
    {
        ct += len[i] / mid;
    }
    return ct >= k;
}

int main()
{
    cin >> n >> k;
    int max_len = -1; // 所有原木的最长的长度，作为右端点

    for (int i = 0; i < n; i++)
    {
        cin >> len[i];
        max_len = len[i] > max_len ? len[i] : max_len;
    }

    int L = -1, R = max_len + 1, mid;
    while (L + 1 != R)
    {
        mid = (L + R) / 2;
        if (check(mid)) // 如果是答案
            L = mid;
        else
            R = mid;
    }

    // L 指向满足要求的答案中最大的答案位置(分界的标记处)
    cout << L << endl;
    return 0;
}

浮点数二分

引入

1、对于两个浮点数，如 $a = 1.1,\ b = 1.1$ ，不能使用==来判断两个浮点数的关系，因为程序可能记录的是 $a = 1.0999999,\ b = 1.1000001$这种形式
2、一种解决方法是：如果程序最后要求保留 $n$ 位小数，就将输入的浮点数扩大 $10^n$ 倍化为整数，以整数方式处理完后再缩小回浮点数
3、以洛谷 P1577为例，这道题与上面二分答案的例题思路一样，只是处理的数据变成了浮点数，答案保留两位小数

代码实现

#include <iostream>
#include <iomanip>
using namespace std;

int n, k;
int len[100001];

// 判断答案是否成立
bool check(int mid)
{
    long long ct = 0;

    if (mid == 0) // 防止除数为 0
        return false;

    for (int i = 0; i < n; i++)
    {
        ct += len[i] / mid;
    }
    return ct >= k;
}

int main()
{
    cin >> n >> k;
    int max_len = -1; // 所有绳子中最长的长度，作为右端点

    for (int i = 0; i < n; i++)
    {
        double t;
        cin >> t;                           // 读取一个浮点数
        len[i] = static_cast<int>(t * 100); // 乘 100 并转换成整数
        max_len = len[i] > max_len ? len[i] : max_len;
    }

    int L = -1, R = max_len + 1, mid;
    while (L + 1 != R)
    {
        mid = (L + R) / 2;
        if (check(mid)) // 如果是答案
            L = mid;
        else
            R = mid;
    }

    // L 指向满足要求的答案中最大的答案位置(分界的标记处)，将答案除以 100 转换回浮点，保留两位小数
    cout << fixed << setprecision(2) << (L / 100.0) << endl;
    return 0;
}

例-跳石头

跳石头

1、以跳石头为例
2、题目需要求最短跳跃距离的最大值，也就是一个最值问题，我们可以通过二分答案将其转换为一个判定问题
3、通过二分答案假设最大值，以此判断这个序列之间需要拿走几块石头，如果拿走数量小于题目要求则答案成立，否则不成立

代码实现

#include <iostream>
using namespace std;

int l, n, k;
int rock[50002];

bool check(int mid)
{
    int ct = 0;    // 拿走了几块石头
    int last = -1; // 拿走的石头后，上一块石头的位置
    for (int i = 1; i <= n + 1; i++)
    {
        // 先前拿走过石头
        if (last != -1)
        {
            // 如果足够距离的话
            if (rock[i] - rock[last] >= mid)
                last = -1; // last 归位
            // 否则距离不够，继续拿走这块石头
            else
                ct++;
        }
        // 之前没拿走石头，if 需要拿走这块石头的话：
        else if (rock[i] - rock[i - 1] < mid)
        {
            ct++;
            last = i - 1;
        }

        // 如果拿走的石头数已经超过 k，说明答案不成立
        if (ct > k)
            return false;
    }
    return true;
}

int main()
{
    cin >> l >> n >> k;

    rock[0] = 0;     // 起点
    rock[n + 1] = l; // 终点
    for (int i = 1; i <= n; i++)
        cin >> rock[i];

    // 二分答案，mid 代表当前最短跳跃距离的最大值
    int L = -1, R = l + 1, mid;
    while (L + 1 != R)
    {
        mid = (L + R) / 2;

        if (check(mid))
            L = mid;
        else
            R = mid;
    }
    cout << L << endl;
    return 0;
}

二分查找

二分答案

浮点数二分

例-跳石头

页底评论