并查集

并查集

1、并查集是一种支持合并和查询操作的集合形式的数据结构，它支持两个集合的合并，并可以查询点与点之间的连通关系
2、并查集只需要一个数组 $pre[]$ 存储点的前导点(父节点)，在初始化时 $pre[i] = i$ ，表示点与自己连通，是单独的连通块，该功能由 $init()$ 函数完成。并查集中还需要一个函数 $root(u)$ ，该操作将找到点 $u$ 所属的连通块(的根节点)。该函数将递归查找 $u$ 的父节点，直至找到根节点
3、对于两个点 $u$ 和 $v$ 的合并操作，只需要将 $u$ 和 $v$ 所属的连通块的其中一个根指向另一个根，即 $pre[root(u)] = root(v)$ ；对于两个点 $u$ 和 $v$ 的查询操作，只需要判断 $u$ 和 $v$ 所属的连通块的根是否相同
4、但前述 $root(u)$ 函数的朴素算法每次都需要查找一整条父节点链，效率太低，可以通过路径压缩优化程序： pre[u] = (pre[u] == u ? u : root(pre[u]))，这样同一连通块在第一次查找后，每个节点都将直接指向当前根节点，提高以后查找的效率，时间复杂度接近 $O(1)$
```
const int N = 1e5 + 10;
int pre[N];

// 初始化函数
void init(int n)
{
    for (int i = 0; i <= n; i++)
        pre[i] = i;
}

// 朴素算法的 root()
int root_(int u)
{
    return pre[u] == u ? u : root_(pre[u]);
}

// 路径压缩的 root()
int root(int u)
{
    return pre[u] = (pre[u] == u ? u : root(pre[u]));
}

// 合并操作
void merge(int u, int v)
{
    pre[root(u)] = root(v);
}

// 查找操作
bool isCon(int u, int v)
{
    return root(u) == root(v);
}
```
连通块问题

1、连通块问题：给定一个无向图，包含 $m$ 个点 $n$ 条边(没有重边和自环)，求图中所有连通块大小，升序输出。如示例中有 $5$ 个点 $2$ 条边，两条边为$\{1, 2\}, \{1, 3\}$，则构成了三个连通块 $\{1, 2, 3\}, \{4\}, \{5\}$，所以升序输出大小 $1 1 3$
2、通过并查集，合并和区分连通块十分容易，如何知道连通块的大小？可以根据桶的思想，用桶统计连通块的大小，再从桶中找出有效答案，排序输出

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
int pre[N], ct[N]; // ct 作为桶，统计连通块的大小

void init(int n)
{
    for (int i = 0; i <= n; i++)
        pre[i] = i;
}

int root(int u)
{
    return pre[u] = (pre[u] == u ? u : root(pre[u]));
}

void merge(int u, int v)
{
    pre[root(u)] = root(v);
}

bool isCon(int u, int v)
{
    return root(u) == root(v);
}

void solve()
{
    int n, m;
    cin >> n >> m;

    init(n);
    for (int i = 1; i <= m; i++)
    {
        int u, v;
        cin >> u >> v;
        merge(u, v);
    }

    // 用桶统计连通块的大小
    for (int i = 1; i <= n; i++)
        ++ct[root(i)];

    vector<int> ans; // 用 ans 记录答案
    for (int i = 1; i <= n; i++)
        if (ct[i]) // 如果根节点为 i 的连通块大小不为 0
            ans.push_back(ct[i]);

    // 排序并输出答案
    sort(ans.begin(), ans.end());
    for (int &it : ans)
        cout << it << ' ';
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

启发式合并

启发式合并

1、连通块问题 2：有 $n$ 个点 $m$ 条边 ($n,m \leq 2 \times 10^5$)。输入点的个数 $n$，给出每个点的权值 $w_i$，再输入边的个数 $m$，接下来每行输入 $u, v$ 表示存在一条由 $u$ 到 $v$ 的无向边。规定每个连通块的权值为块中所有点权值的异或和，求图中权值最大的连通块的权值
2、启发式合并：并查集的每个节点多了一个 $sz$，根节点的 $sz$ 表示连通块的大小，其余的 $sz$ 在被使用不再是根节点后无实际作用。启发式合并不能使用路径压缩，其root()只能使用朴素版本，其核心在于merge()时只能让小连通块指向大连通块 (通过 $sz$ 实现)。为方便，实现中用 $rx, ry$ 分别记录 $x, y$ 的根
3、先前的路径压缩虽然更快但会破坏图的结构，如果要保留原图且追求速度，只能使用启发式合并。启发式合并的小指向大保证了非必要时不增加查询层数，因而降低了朴素root()的时间复杂度至 $O(\log n)$。此外，路径压缩不能撤销(回到上一步)，因为其破坏了原图

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
int w[N];
int pre[N], sz[N]; // 并查集，连通块大小

// 只能使用朴素版本
int root(int x)
{
    return pre[x] == x ? x : root(pre[x]);
}

// 启发式合并
void merge(int x, int y)
{
    int rx = root(x), ry = root(y);
    // 如果是同一连通块，退出
    if (rx == ry)
        return;

    // 令 rx 为小连通块，检查是否成立，不成立就交换位置
    if (sz[rx] > sz[ry])
        swap(rx, ry);
    pre[rx] = ry;     // 使 rx 连向 ry
    sz[ry] += sz[rx]; // 更新连通块大小
}

void solve()
{
    int n, m;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> w[i];

    // 初始化并查集
    for (int i = 1; i <= n; i++)
        pre[i] = i, sz[i] = 1;

    cin >> m;
    while (m--)
    {
        int x, y;
        cin >> x >> y;
        merge(x, y);
    }

    // 把节点权值异或到根上，如果是根，不用操作
    for (int i = 1; i <= n; i++)
        if (pre[i] != i)
            w[root(i)] ^= w[i];

    // 统计答案，如果是根，取大
    int ans = 0;
    for (int i = 1; i <= n; i++)
        if (pre[i] == i)
            ans = max(ans, w[i]);
    cout << ans;
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

可撤销并查集

可撤销并查集

1、可撤销并查集：输入节点个数 $n$ 和询问次数 $q$ ($n \leq 10^6, q \leq 10^5$)。对于每个询问：输入 $1\ x\ y$ 将 $x\ y$ 连通，输入 $2$ 撤销上一次操作(若已经全部撤销则不操作)，输入 $3\ x\ y$ 查询 $x\ y$ 是否连通，输出 YES 或 NO
2、可撤销并查集可以撤销到上一步操作(并不是撤销到任意一步，这种情况需要可持久化并查集)，其使用启发式合并。回想合并时 merge() 操作，核心变化其实是 $pre[rx] = ry$ 和 $sz[ry] += sz[rx]$ ，那么就可以用一个pair存储 $\{rx, ry\}$ ，回到上一步只需要令 $pre[rx] = rx$ 重新指向自己，再 $sz[ry] -= sz[rx]$ 撤销更改。撤销到上一步恰好适合用栈维护，所以用 stack 维护 pair

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
int pre[N], sz[N];         // 并查集，连通块大小
stack<pair<int, int>> stk; // 维护撤销 pair

// 只能使用朴素版本
int root(int x)
{
    return pre[x] == x ? x : root(pre[x]);
}

// 启发式合并
void merge(int x, int y)
{
    int rx = root(x), ry = root(y);
    // 如果是同一连通块，退出
    if (rx == ry)
        return;

    // 令 rx 为小连通块，检查是否成立，不成立就交换位置
    if (sz[rx] > sz[ry])
        swap(rx, ry);

    // 存储当前状态
    stk.push({rx, ry});

    pre[rx] = ry;     // 使 rx 连向 ry
    sz[ry] += sz[rx]; // 更新连通块大小
}

// 撤销到上一状态
void undo()
{
    if (stk.empty())
        return;

    // 取出 rx, ry
    auto [rx, ry] = stk.top();
    stk.pop();

    // 还原
    pre[rx] = rx;
    sz[ry] -= sz[rx];
}

void solve()
{
    int n, q;
    cin >> n >> q;

    // 初始化并查集
    for (int i = 1; i <= n; i++)
        pre[i] = i, sz[i] = 1;

    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            int x, y;
            cin >> x >> y;
            merge(x, y);
        }
        else if (op == 2)
            undo();
        else
        {
            int x, y;
            cin >> x >> y;
            cout << (root(x) == root(y) ? "YES" : "NO") << '\n';
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

带权并查集

带权并查集

1、小 e 的可乐：输入可乐瓶数 $n$ 和操作次数 $q$，这些可乐中有两种种类，但目前无法区分。对于每个操作：输入 $1\ x\ y$ 表示 $x\ y$ 是不同种可乐，输入 $2\ x\ y$ 判断 $x\ y$ 是否是同种可乐，输出 YES、NO 或 Unknown
2、带权并查集常用于处理种类问题，其使用启发式合并，每个节点上有一个权值，表示它与它父亲的关系，在该题用 $d[]$ 表示(两点距离)。如果给出两个点不同，便记录它们的距离为 $1$ 并连通，根据距离的奇偶可以判断是否是同种：理想条件下，例如 $1 2$、$2 3$ 不同，那么 $2$ 指向 $1$ 且 $d[2] = 1$，$3$ 指向 $2$ 且 $d[3] = 1$ (注意 $d[]$ 表示与父节点的关系)，那么：$1 3$ 距离为 $2$ 是同种可乐，$2 3$ 距离为 $1$ 不是同种，$1 4$ 不连通所以未知
3、但是，启发式合并时，不会让 $3$ 指向 $2$，而是指向根节点 $1$。又如下图例，使 $2$ 指向 $3$，在启发式合并是使 $1$ 指向 $4$ (根指向根)，那么如何确定 $d[rx]$ 的值？借用向量的思想：如下简化后图例，要使 $x$ 指向 $y$，便有 $x y$ 距离为 $1$ (父子节点间距离为 $1$，实际不连接)，那么使 $rx$ 指向 $ry$ 后，有 $1 = getd(x) + d[rx] - getd(y)$ (向量的思想)，其中，getd()用于获取当前节点与根节点的距离，注意不能替换为 $d[]$，因为其只表示当前节点与父节点的距离，而到根节点之间可能有其他的中间节点。对上式进行等式变换，可以得到 $d[rx] = 1 - getd(x) + getd(y)$。最后判断时，判断 $getd(x) - getd(y)$ (即 $x, y$ 的距离)的奇偶即可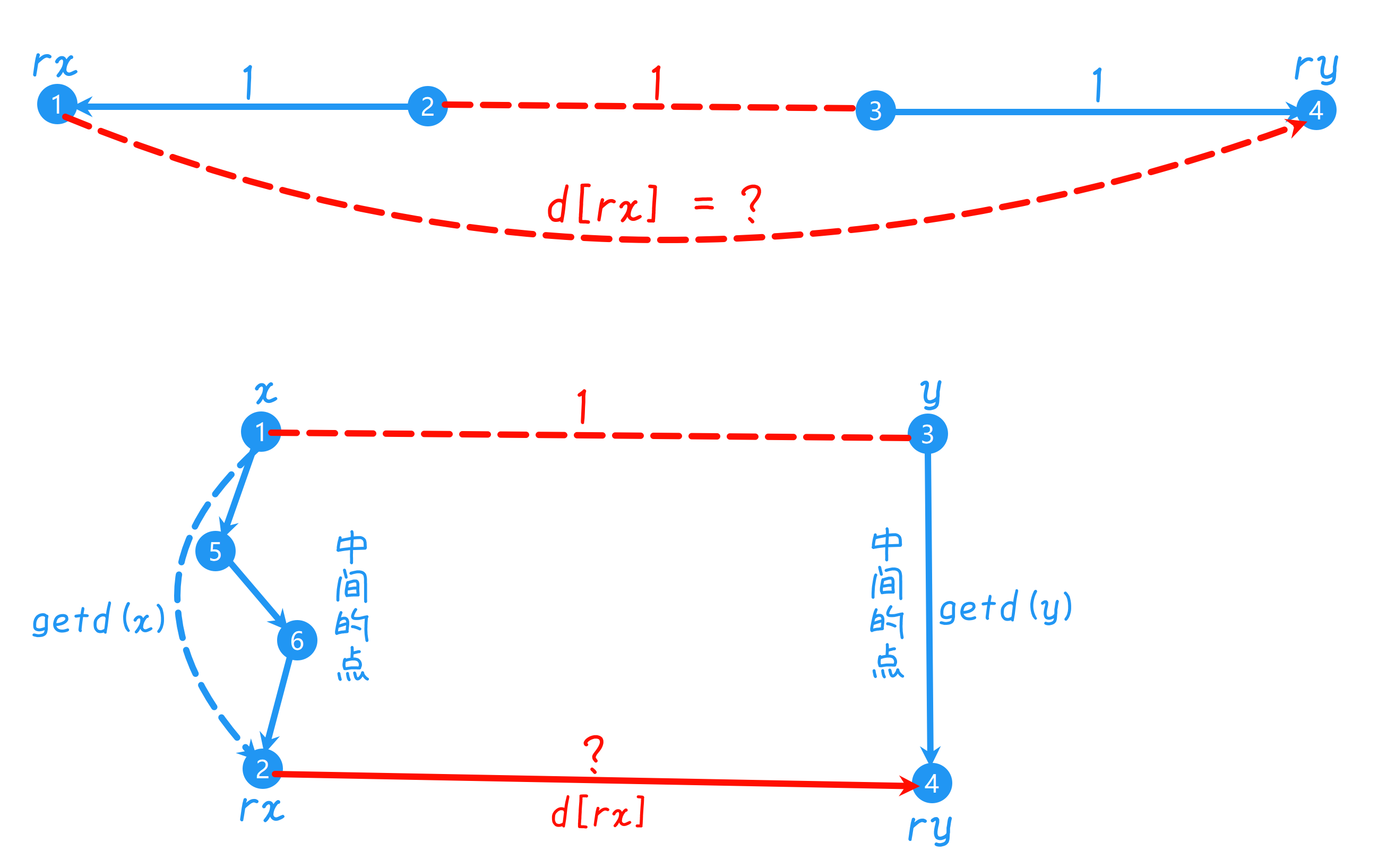

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
int pre[N], sz[N], d[N]; // d[x] 表示 x 与父节点的距离

int mo(int x)
{
    return (x % 2 + 2) % 2;
}

// 获取 x 与根节点的距离
int getd(int x)
{
    int res = 0;

    // 只要 x 不是根节点
    while (pre[x] != x)
    {
        res += d[x];
        x = pre[x];
    }
    return res;
}

int root(int x)
{
    return pre[x] == x ? x : root(pre[x]);
}

void merge(int x, int y)
{
    int rx = root(x), ry = root(y);

    if (rx == ry)
        return;

    if (sz[rx] > sz[ry])
        swap(rx, ry);

    pre[rx] = ry;
    sz[ry] += sz[rx];
    d[rx] = 1 - getd(x) + getd(y); // 更新 d[rx]
}

void solve()
{
    int n, m;
    cin >> n >> m;

    // 初始化
    for (int i = 1; i <= n; i++)
        pre[i] = i, sz[i] = 1, d[i] = 0;

    while (m--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            int x, y;
            cin >> x >> y;
            merge(x, y);
        }
        else
        {
            int x, y;
            cin >> x >> y;

            int rx = root(x), ry = root(y);
            if (rx != ry)
                cout << "Unknown\n";
            else if (mo(getd(x) - getd(y)) == 1)
                cout << "NO\n";
            else
                cout << "YES\n";
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

并查集

启发式合并

可撤销并查集

带权并查集

页底评论